Velocidad de escape y agujeros negros

Prueba a lanzar algo hacia arriba. Seguramente ascienda unos metros y despúes vuelva a caer. Cuanto más fuerte lo tires, más tiempo tarda en caer, ¿no? ¿Nunca te has preguntado a qué velocidad lo tienes que lanzar para que no caiga jamás? Si es así, ¡continua leyendo esta entrada!

De lo que vamos a hablar es de la velocidad de escape: la velocidad mínima que debe de tener un objeto para escapar de la atracción gravitatoria de otro. ¿Cómo podemos calcularla?

Si lanzamos un objeto hacia arriba desde la Tierra, se irá frenando poco a poco hasta que se frene y caiga. Para que el objeto no caiga nunca, su velocidad deberá ser tal que solo llegue a frenarse cuando se encuentre a una distancia infinita de nuestro planeta (supongamos que no influyesen en el objeto otros astros, aunque no es así).

Por tanto, en el infinito, su velocidad tiene que ser 0, por lo que su energía cinética (relacionada con la velocidad) también será 0. ¿Cuánto valdrá su energía potencial?

Dado que consideramos que el objeto se encuentra a una distancia infinita, su energía potencial será 0, al igual que su energía cinética.

Como la gravedad es una fuerza conservativa, la energía mecánica del objeto lanzado (la suma de la cinética y la potencial) es constante, y vale 0. Por lo tanto, se deduce que ambas energías son iguales. Igualandolas obtenemos:

En este caso, R es el radio de la Tierra, G es la constante de la gravitación universal y Mt es la masa de la Tierra. Sustituyendo, nos da que la velocidad de escape de un objeto (no importa su masa) desde la superficie de la Tierra es de unos 11 Km/s.

Por tanto, si consigues lanzar algo hacia arriba a esa velocidad (o mayor), despídete de él...

Los lectores más avispados os preguntaréis qué pasa en un agujero negro. Un agujero negro es un "objeto" que crea un campo gravitatorio tan potente que ni la luz puede escapar de él. Quiere decir que posee una velocidad de escape superior a la de la luz. Igualando la fórmula obtenida anteriormente a la velocidad de la luz:

Hemos obtenido una fórmula en la que R es el radio mínimo de un agujero negro de masa M. Este "radio mínimo" se conoce como radio de Schwarzschild. En el caso de la Tierra, R vale 0,88 cm. ¿Qué significa esto? Significa que si redujésemos todo el planeta Tierra a un tamaño menor al de una canica, su densidad sería tal que se convertiría en un agujero negro, ya que su velocidad de escape sería igual o superior a la de la luz, y como sabemos que nada puede superar esa velocidad, nada* puede escapar de un agujero negro.

A partir de lo hasta aquí obtenido, podemos deducir que la densidad de un agujero negro viene dada por:

Por tanto, la densidad depende del radio: a mayor radio, menor densidad. Un agujero negro de radio 500.000 veces mayor al de la Vía Láctea podría tener una densidad inferior a la del agua.

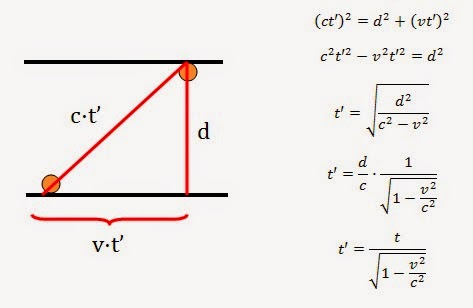
Esto tiene que ver mucho con la Teoría General de la Relatividad, que dice que el tiempo va ralentizándose a medida que la intensidad del campo gravitatorio aumenta. Cuando esta intensidad equivale a la de un agujero negro, el tiempo se detiene (para un observador situado fuera del agujero negro).

Gracias por haber leído esta entrada. No os olvidéis de votar mi blog en la categoría de Ciencia en los Premios Bitácoras. Votar es muy fácil. Si no sabes cómo, clic aquí.

Hasta la próxima!

*Sin tener en cuenta la supuesta Radiación de Hawking.

Resolviendo la paradoja de Aquiles y la tortuga

Zenón de Elea fue un filósofo griego muy conocido por plantear numerosas paradojas relacionadas con el movimiento. De entre todas ellas, la más famosa puede que sea la de Aquiles y la tortuga. 

Aquiles decide echar una carrera a una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.

Todos sabemos que Aquiles ganará de sobra la carrera, igual que pensaba Zenón. Zenón planteó 40 paradojas de este estilo, debatiendo sobre el espacio, el tiempo y el movimiento. Proponía estos ejercicios mentales para reducir al absurdo las teorías de que la suma de infinitos números tenga que dar infinito. 

Si la suma de infinitos sumandos siempre fuese igual a infinito, Aquiles nunca ganará la carrera, pero esto matemáticamente y físicamente no es así. 

Supongamos que la velocidad de la tortuga es de 1 m/s, la velocidad de Aquiles es de 10 m/s y la ventaja inicial es de 100 m. En solo 10 segundos, Aquiles habrá alcanzado el punto desde el que sale la tortuga, y esta habrá avanzado 10 metros más. Esos 10 metros los recorre Aquiles en 1 segundo, pero la tortuga habrá avanzado 0,1 metros más...y así sucesivamente. Lo que plantea la paradoja es que 10 + 1 + 0,1 + ... da como resultado infinito, pero eso es incorrecto.

Cada vez, Aquiles tarda 10 veces menos en recorrer el trozo que lo separa de la tortuga. Esta fórmula nos puede ayudar a conocer todos los tiempos empleados (progresión geométrica decreciente):

Sucesión de tiempos empleados
expresada en segundos

Aplicando una fórmula que no vamos a demostrar ahora (fórmula de la suma de los infinitos términos de una progresión geométrica decreciente), podemos hallar la suma de esos tiempos. La demostración se realizaría restando a la suma de todos los términos, la suma multiplicada por la razón, pero por comodidad no lo vamos a hacer.

Como vemos en la imagen superior, la suma de 10 + 1 + 0,1...da como resultado 11,1 segundos. Aunque haya infinitos sumandos, el resultado es finito. Esto demuestra que Aquiles alcanza a la tortuga y lógicamente gana la carrera.

Podemos resolverlo también utilizando las leyes del movimiento, ya que conocemos las velocidades de ambos corredores la diferencia de posiciones. Igualando las posiciones conseguimos despejar el tiempo transcurrido en cruzarse.

Por lo tanto, una suma de infinitos términos decrecientes puede dar un resultado finito, como en este caso.

Un saludo, nos vemos en la próxima. No os olvidéis de compartir esta entrada!

Efecto Doppler Relativista

Antes de comenzar, recomiendo leer la entrada anterior (Fórmulas del Efecto Doppler). Gracias al Efecto Doppler se pudo comprobar la Expansión del Universo. En la entrada de hoy combinaremos lo de las tres últimas entradas con la Teoría de la Relatividad Especial de Albert Einstein.

En la entrada anterior hemos considerado el espacio y el tiempo como dimensiones aisladas y absolutas. ¿Pero qué pasa cuando la aproximación entre fuente y observador se aproxima a la velocidad de la luz? Tal y como habíamos dicho en la serie sobre Relatividad Especial, el espacio y el tiempo dependen uno del otro y no son absolutos, sino que dos observadores que se muevan a distintas velocidades pueden medir tiempos y espacios diferentes, y todo ello porque la velocidad de la luz es constante para cualquier observador. A físicos como Albert Einstein o Hendrik Lorentz le debemos estas maravillas.

Recordemos que la Teoría de la Relatividad nace de la idea de que la luz viaja siempre a la misma velocidad en el vacío, tal y como demostró el experimento de Milchelson y Morley.

Supongamos que fabricamos un reloj que funciona con un fotón (partícula asociada a la luz) que rebota entre dos espejos. Cuando rebota, va haciendo tic-tac, como en el del vídeo inferior.

Enlace desde móviles

La distancia d entre los dos espejos es igual a c·t, es decir, la velocidad de la luz por el tiempo que tarda en llegar de un espejo a otro. Dicho de otro modo, el tiempo es igual al espacio entre la velocidad: t = d/c.

Ahora supongamos que introducimos ese reloj en una nave espacial que se mueve a velocidad v. Un astronauta dentro de la nave seguirá oyendo esos tic-tac con la misma frecuencia, ¿pero cómo verá eso una persona desde la Tierra?

Enlace desde móviles

El fotón visto para un astronauta dentro de la nave, sube y baja en línea recta. Pero visto desde fuera, realiza un movimiento en zig-zag, como muestra la imagen inferior. Mediante una serie de sencillas operaciones, deducimos que el tiempo que medía el observador en movimiento (t) es inferior al que mide el observador en reposo (t'):

Eso significa que el tiempo transcurre relativamente más lento para una persona que se mueva que para una en reposo. Si alguien viajase por el espacio a una velocidad de 260.000 km/s durante 50 años, al volver a la Tierra parecería que solo ha envejecido 25 años. A velocidades pequeñas (coches, meteoritos, misiles...), esa dilatación temporal es imperceptible. Necesitaríamos viajar más de 5 millones de años sin parar en coche para que nuestro reloj se atrase solo 1 segundo...antes se queda sin pila...

Una vez repasada la dilatación temporal, podemos comenzar con nuestros típicos ejercicios de imaginación:

Imaginemos que una nave espacial que se mueve hacia nosotros con una velocidad v emite pulsos luminosos a ritmo constante. A nosotros nos interesa calcular la longitud de onda de esos pulsos, entonces contamos el número de ellos que suceden en un tiempo t, y también calculamos cuánto espacio recorre la nave en ese tiempo. Si llamamos N al número de pulsos contados en un intervalo de tiempo t, la longitud de onda será:

A partir de la longitud de onda, hallamos la frecuencia:

Según la Relatividad Especial, la imagen inferior relaciona el periodo medido desde el sistema de referencia del observador (T) y el de la fuente (T'). 

Combinando las ecuaciones (I) y (II), obtenemos:

Racionalizando la expresión superior y simplificándola:

Tenemos que recordar que según el Principio de Relatividad, el movimiento es relativo. Imaginemos que viajamos en coche. Según este principio, es equivalente decir que el coche se mueve respecto a la carretera que decir que la carretera se mueve debajo de las ruedas del coche. Por tanto, no podemos saber si es la fuente la que se mueve o si somos nosotros, solo podremos decir que existe un movimiento.

Dependiendo si fuente y observador se alejan o acercan entre sí, aquí quedan las fórmulas para la frecuencia y la longitud de onda:

Si aumenta la frecuencia, disminuye la longitud de onda y viceversa, ya que c es constante para cualquier sistema de referencia. Otra forma de ver las ecuaciones superiores es considerar positiva la velocidad cuando es de aproximamiento y negativa cuando se alejan, teniendo solo que usar la primera.

Dicho esto, solo nos queda aclarar lo dicho en la entrada sobre la Expansión del Universo.  

Si una estrella se aleja de nosotros, según las ecuaciones superiores, su frecuencia debería disminuir. Por eso mismo se produce el corrimiento al rojo, porque el rojo es el color de menos frecuencia del espectro visible. 

Por el contrario, si una estrella se acerca, se produciría el corrimiento al azul debido al mismo efecto.

Para terminar, un "problema-chiste": Un físico iba pensando en sus ecuaciones sobre la Teoría de Supercuerdas mientras conducía, como cualquier mañana normal. De repente se da cuenta de que le persigue la policía por saltarse un semáforo en rojo, pero como es físico, intenta pensar una escusa rápida. Le dice al policía que no vio el semáforo rojo, sino verde, debido al efecto Doppler. De todos modos, el agente le puso una multa por exceso de velocidad...¿A qué velocidad iba nuestro amigo el físico? Intenta calcularla y deja la respuesta en los comentarios. (La longitud de onda del rojo es de 650 nm y la del verde es de 520 nm). Este problema y su solución están en la sección Ingenio.

Demostración desde la matriz de Lorentz

La ecuación de onda electromagnética, en la imagen inferior, es una invariante relativista.

Luego la fase del campo eléctrico también ha de serlo. Definimos el cuadrivector K como:

Por lo que, en la dirección del movimiento tenemos que:

Y en direcciones perpendiculares a la del movimiento:

Y aquí acaba esta serie de 4 entradas sobre el Efecto Doppler. Si te ha gustado, no olvides compartir y dejar comentarios. Nos "vemos" en la próxima.

Un saludo!

Fórmulas del Efecto Doppler

En entradas anteriores (El Efecto Doppler y La Expansión del Universo) mencionamos una ecuación que nos permitía relacionar la frecuencia emitida (como el sonido "real" que sale de la sirena de una ambulancia) con la frecuencia percibida (sonido "distorsionado" que oímos). En la entrada de hoy vamos a intentar razonar por qué es así:

A. Observador en movimiento y fuente en reposo

El observador somos nosotros, los que percibimos, por ejemplo, un sonido. La fuente es el instrumento que emite ese sonido. Imaginemos un piano sonando y nosotros acercándonos hacia él. Las ondas que emite tienen una longitud de onda constante, pero al acercarnos, la frecuencia con la que nos llegan aumenta. Ahora intentaremos sacar una fórmula que relacione ambas frecuencias dependiendo de la velocidad con la que nos acerquemos (o alejemos):

Esta será la notación que usaremos en la entrada de hoy:

Como la longitud de onda no varía, igualaremos la longitud emitida con la percibida, y despejando obtendremos la ecuación encuadrada:

Cabe destacar que si el observador se aleja de la fuente, el signo "+" del numerador se transforma en un "-", por lo que la frecuencia al alejarnos de un sonido disminuirá y al acercarnos, aumentará.

B. Fuente en movimiento y observador en reposo

Si la fuente se aleja respecto a nosotros, cada pulso nos llega desde más lejos que el anterior, por lo que la longitud de onda aumentará de esta forma:

En el caso de que la fuente se acerque, la longitud de onda disminuiría, por tanto la frecuencia aumentaría y en el denominador de la fórmula encuadrada superior habría que poner un "-" en vez de un "+".

Fórmula General

Vamos a deducir una fórmula general en el caso de que tanto fuente como observador estén en movimiento.

Y como es lógico, combinándolas todas obtenemos la general:

El signo del numerador será "+" cuando el observador se acerque a la fuente, y "-" cuando se aleje. El signo del denominador será "-" cuando la fuente se acerque al observador y "+" cuando se aleje.

En la próxima entrada hablaremos sobre el Efecto Doppler Relativista. 

Hasta entonces! Y no os olvidéis de compartir y comentar ;)

¿Cómo descubrieron Neptuno?

Una vez que sir Isaac Newton encontró su famosa Ley de la Gravitación Universal, se pensaba que todo en el universo se comportaría de forma predecible y que tantos los planetas como todos los astros seguían trayectorias lógicas y que se deducían a partir de las leyes de Kepler y Newton.

El Universo se contemplaba como una enorme máquina de relojería, y tenían la visión de Dios como un implacable matemático diseñador de tal obra. Nacería así el determinismo científico, teoría filosófica que básicamente niega la existencia de la libertad. Se pensaba que todo en el Universo era entendible según esas leyes que ya se poseían, y por tanto la conducta humana era también predecible, pero mucho más compleja.

Pierre Simon Laplace postularía su tesis del Demonio de Laplace, un hipotético demonio capaz de conocer la posición y momento de todas las partículas del universo. Así, podría calcular sus posiciones y momentos en cualquier otro momento. 

Conociendo las distancias interplanetarias y las masas de cada planeta, podríamos calcular la velocidad de traslación de cada astro de nuestro Sistema Solar simplemente igualando la fuerza centrífuga (hacia fuera) de cada planeta debido al movimiento elíptico que describen con la atracción del Sol. Por ejemplo, si yo describo una rotonda en coche, para que el vehículo no vuelque en la curva, la fuerza de rozamiento del suelo debe ser igual a la fuerza centrífuga. Lo mismo ocurre con los planetas.

La fuerza centrífuga, para que la Tierra no salga despedida, es igual a la atracción gravitatoria del Sol

Efectivamente, la fuerza centrífuga tiene un valor muy parecido al de la atracción gravitatoria. Recordemos que la órbita es una elipse, no una circunferencia.

Aplicando esta definición planeta por planeta, comprobaron que la Ley de la Gravitación de Newton se ajustaba perfectamente a las predicciones, excepto en Urano. La órbita de Urano presentaba ciertas perturbaciones, y comenzó una desconfianza en la teoría de Newton, que parecía estar fallando.

En la década de 1840, John Couch Adams y Urbain le Verrier tuvieron la siguiente idea: puede que exista un cuerpo, más allá de la órbita de Urano, que por interacción gravitatoria desvíe la trayectoria de este último. De ser así, podríamos encontrarnos frente al octavo planeta del Sistema Solar.

Urbain le Verrier

Manos a la obra. De manera independiente trabajaron intentando hallar la masa, posición, tamaño y distancia de ese hipotético planeta. En 1846 concluyeron sus cálculos, prediciendo las coordenadas donde se encontraría la noche del 23 de septiembre de 1846. Efectivamente, ese día fue observado Neptuno, el primer planeta que anteriormente se había descubierto matemáticamente.

Neptuno

Pero aquí no acaba la cosa: Urano no era el único planeta que presentaba anomalías en su órbita. También era conocido el caso de la desviación del perihelio de Mercurio. Se atribuía a una mala medida, pero le Verrier volvió a plantear el mismo argumento que aplicó en el caso de Urano. Pensó que alomejor podría existir un planeta entre el Sol y Mercurio, al que bautizó como Vulcano, que desviase también su órbita. En este caso, se equivocó. La órbita de Mercurio, efectivamente, no encajaba dentro de la Teoría de Newton. Tuvo que ser en 1915 cuando Einstein encontrase la solución.

Debido a la enorme masa solar y el campo gravitatorio que genera, es necesario tener en cuenta los factores relativistas de la Teoría de la Relatividad General de Einstein, ya que la de Newton no es válida en esos casos. Uno de los hitos de la teoría de Einstein fue esa, explicar las anomalías de la órbita de Mercurio (entre multitud de fenómenos que predicen sus ecuaciones). También fue demostrada experimentalmente durante el famoso eclipse de 1919, donde se comprobó que la luz de estrellas situadas detrás del Sol se curvaba al pasar cerca suyo. La luz, aunque no tenga masa, posee un momento lineal asociado a su frecuencia, por lo que también deforma el espacio-tiempo y puede ser desviada.

Y así es como se descubrió un planeta gracias a la valiosísima herramienta que son las matemáticas. Hoy en día se descubren planetas de esta manera, al igual que los agujeros negros se encuentran observando cómo se comporta la materia a su alrededor. Otro método de detectar planetas es estudiar los cambios de brillo de estrellas cuando el planeta pasa por delante.

Visita la entrada Deducción de la Tercera Ley de Kepler.

Espero que os haya gustado esta entrada. Compartidla y comentar.
Un saludo,
Gabriel.

Paradoja de los Gemelos

Y finalmente llegamos al final de esta serie dedicada especialmente a Relatividad Especial. Si quieres leer el resto de entradas sobre este tema, te invito a que hagas clic en el siguiente enlace, donde están todas agrupadas: Serie de Relatividad Especial.

Hoy vamos a tratar la Paradoja de los Gemelos. Antes de todo, veamos en qué consiste:

"Dos hermanos gemelos deciden hacer un peculiar experimento: uno de ellos es astronauta, y se embarca en un viaje espacial a velocidades próximas a la de la luz. Para el que permaneció en la Tierra, el astronauta ha sido el que se ha movido, por tanto al regresar habrá envejecido menos que él (de acuerdo con la dilatación temporal que sufre a esas velocidades). Pero para el astronauta, el que se ha movido respecto a él ha sido el resto del Universo...por tanto al volver, el que menos habrá envejecido habrá sido el que permaneció aquí".

Aquí reside la paradoja, ya que lo que miden los dos no tiene sentido en el momento en el que se encuentran. Si analizamos a fondo el experimento, veremos qué gemelo tiene razón. ¿Te apuntas?

Antes de nada, recordemos que a grandes velocidades el tiempo se ralentiza, el espacio se contrae y la masa aumenta. Vamos a observar el experimento desde el punto de referencia del gemelo astronauta primero, y finalmente el otro gemelo. De este modo queremos saber qué ocurre exactamente y cuál de los dos envejece más. Vamos a añadir un matiz: tanto el astronauta como su hermano tienen una linterna con la que envían un destello cada segundo a su hermano.

El astronauta decide embarcarse en su travesía espacial de 10 años luz a 261.000 km/s (he escogido este valor para simplificar las cuentas al final). El astronauta no mide 10 años luz, sino que debido a la contracción espacial que experimenta, para él el trayecto es de 5 años luz. A la velocidad que lleva, debería tardar 11,5 años ida y vuelta en completar el trayecto. Sin embargo, para el que permanece en la Tierra no es así...

Aunque el hermano que se queda en la Tierra encienda y apague su linterna cada segundo, el astronauta no ve esos destellos cada segundo, porque cada segundo la luz tiene que recorrer una distancia de 261.000 km más (el espacio que recorre su nave en un segundo). Debido a esto, los destellos se ralentizan cada 1,87 segundos...y si aplicamos la fórmula de dilatación temporal...los destellos se producirán cada 3,74 segundos.

Hemos dicho que para el astronauta, el tiempo de ida y vuelta son 11,5 años, entonces en ir emplearía la mitad, un total de 5,75 años. Como el tiempo en la Tierra transcurre 3,74 veces más lento, el tiempo que habrá medido el hermano de la Tierra será 5,75/3,74...es decir, 1,5 años.

Cuando el astronauta llega a su destino y se da la vuelta, el proceso se invierte. Cada segundo, la luz tiene que recorrer 261.000 km menos, lo que provoca que esos destellos los perciba cada 0,26 segundos teniendo en cuenta la dilatación temporal. Entonces, los 5,75 años de vuelta de la nave para nosotros son como 21,5 años, el resultado de dividir 5,75/0,26.

Astronauta: 5,75 + 5,75 = 11,5 años

Tierra: 1,5 + 21,5 = 23 años

Si hacemos cuentas, el astronauta ha vivido 11,5 años en total y nosotros en la Tierra hemos vivido 23 años, el doble, exactamente el mismo resultado que obtendríamos según la transformación de Lorentz.

Según la primera parte de este experimento, el que menos envejece es el astronauta.

Ahora vamos a centrarnos en el hermano que permanece en nuestro planeta. Al igual que antes, los destellos de su hermano le llegan cada 3,74 segundos. La distancia que recorre su gemelo son 10 años luz a un 87% de la velocidad de la luz, entonces la nave tarda 11,5 años "terrestres" en llegar al destino.

Cuando el astronauta llega al final de la travesía y se da la vuelta, en la Tierra vamos a seguir notando los destellos cada 3,74 segundos durante 10 años más, porque se encuentra a 10 años luz de nosotros. Eso quiere decir que pasamos un total de 21,5 años percibiendo los destellos, lo que para el astronauta serían 5,7 años.

Como el viaje de vuelta dura 11,5 años (10 años luz a 261.000 km/s), y 10 de esos años los percibimos cada 3,74 segundos, quedan 1,5 años. A partir de ese momento, desde la Tierra comenzamos a percibir los destellos aceleradamente, porque ya ha llegado el último que se emitió desde el punto más lejano a 10 años luz. Durante esos 1,5 años, los destellos se producen cada 0,26 segundos. Eso quiere decir que para el tripulante de la nave, ese año y medio equivale a 1,5/0,26 = 5,7 años.

Astronauta: 5,7 + 5,7 = 11,5 años

Tierra: 11,5 + 10 + 1,5 = 23 años

Si echamos cuentas, el astronauta ha vivido 11,5 años y en la Tierra han pasado 23 años. Exactamente el mismo resultado que en el caso anterior. Aquí queda resuelta la paradoja.

El gemelo que envejece menos es el astronauta.

En ambos casos se cumple que el que menos envejece es el astronauta, tal y como predicen las ecuaciones de Lorentz y Einstein.

No hemos tenido en cuenta la dilatación temporal producida por la gravedad, que también afectaría al experimento. El gemelo de la Tierra se encuentra en un sistema acelerado constante (la aceleración de la gravedad sería g = 8,81 m/s2), pero el astronauta también tendría que acelerar para lograr tales velocidades, por lo que los datos del experimento podrían variar teniendo en cuenta estas consideraciones.

Aquí llegamos al final de la serie dedicada a Relatividad Especial. Espero que os haya gustado, y como ya sabéis, aquí abajo podéis dejar comentarios.

¡Un abrazo científico!

Aumento de masa

Sí amigo, has leído bien...la masa aumenta...

En entradas anteriores hemos visto cómo se dilata el tiempo (léelo aquí) y como se contrae el espacio (léelo aquí). Al igual que estas magnitudes, la masa no es una constante universal para cualquier sistema de referencia. Dicho bien, lo que ocurre es que el momento lineal de una partícula con masa a grandes velocidades, es proporcional al inverso del factor ß que habíamos visto en entradas anteriores, es decir, que el aumento del momento dependiendo de la velocidad no es una recta, si no que se curva tendiendo a infinito cuando la velocidad iguala a la de la luz. Para la mecánica newtoniana esto no era así, y la masa era constante. De este modo definíamos momento lineal o cantidad de movimiento como el producto de la masa por la velocidad. En los choques elásticos, el momento se conservaba.

Vamos a hacer un experimento mental para entender por qué aumenta la masa:

Juan y María se mueven por el espacio en sentido contrario y de forma paralela, a una velocidad constante y próxima a la de la luz, tal como vemos en la imagen inferior.

Como son movimientos a velocidad constante, cada uno estará parado "para él mismo", y verá solo moverse al otro. Es como cuando vamos en coche y pasa al lado nuestro otro vehículo en dirección contraria. En un momento dado, ambos lanzan hacia el otro una pelota, de tal modo que la velocidad de la bola medida por el que la lanza es la misma que la velocidad de la otra medida por el otro. Es decir, Juan lanza hacia María la pelota a 10 m/s (por ejemplo), y María se la lanza a Juan a la misma velocidad. Si observamos el experimento como si María fuese la observadora en reposo y el que se moviese fuera Juan (consideramos que la velocidad de Juan hacia María es un 87% de la de la luz), dado que el tiempo de Juan (y su bola) transcurre para María de forma más lenta, la velocidad horizontal de la bola que lanza Juan es menor. Si la bola llevase un reloj, para Juan el tiempo de su bola transcurriría "normal", pero para María ese tiempo iría más lento. Si Juan lanza la bola a 10 m/s, para María esa bola recorre 10 m cada 2 segundos, o lo que es lo mismo, 5 m/s (teniendo en cuenta la dilatación temporal).

Visto desde el sistema de referencia de Juan, ocurre lo mismo...son experimentos simétricos: Juan se nota a sí mismo quieto, y María es la que se mueve. Juan lanza la bola a 10 m/s y ve aproximarse la de María a 5 m/s.

Volvamos al sistema de referencia de María. Ella ha lanzado su pelota a 10 m/s contra la de Juan a 5 m/s. Dado que en ese choque se conserva el momento lineal (p = m·v) y como cada bola vuelve a las manos de su dueño después del choque (por lo que los momentos de cada bola son iguales) y además su velocidad horizontal es diferente (siendo la pelota de Juan más lenta), su masa debe ser mayor para conservar la igualdad.

Como Juan se mueve a un 87% de la velocidad de la luz con respecto a María, el tiempo de Juan visto desde el sistema de referencia de María transcurriría dos veces más lento: cada dos segundos de vida de María equivaldría a un segundo en la vida de Juan. Debido a esto, el sistema de Juan (él, su reloj, su bola...) van más lento. Como al lanzar la bola horizontalmente va mas lento (menos velocidad) para chocar y acabar desplazándose lo mismo que la de María, debe tener dos veces más masa.

Podemos imaginar que choca una bola de bolos con una canica. Si van igual de rápido, al chocar, la canica retrocederá más. Esto se debe a que la de bolos es más pesada, y su momento p es mayor. En nuestro experimento retroceden ambas igual, y como una de ellas se mueve la mitad de rápido...para equilibrar la ecuación su masa deberá ser el doble. En la imagen inferior podemos ver la conservación del momento teniendo en cuenta solo las velocidades verticales.

Es decir, que si una persona de 80 Kg se pone a correr, su masa a esa velocidad aumentaría hasta los 80,00000000000001 Kg.

La ecuación que relaciona la masa en reposo (mo) con la masa (m) a una velocidad v es:

Si la velocidad v tiende a c, la masa m tiende a infinito...y como la fuerza necesaria para mover esa masa infinita también sería igual a infinito, la energía sería lógicamente INFINITA.

Por consiguiente, para conseguir que una partícula con masa alcance la velocidad de la luz, es necesario un aporte infinito de energía, por eso una partícula con masa no puede sobrepasar ni alcanzar c. Una partícula con masa nunca podrá alcanzar la velocidad de la luz para ningún sistema de referencia, y la luz no puede reducir su velocidad para ningún otro.

En el siguiente video podremos ver otro modo de entender por qué no es posible superar la velocidad de la luz, además de otras nociones curiosas que os recomiendo ver sobre Relatividad:

Para ver el vídeo desde un móvil, clic aquí.

Como la hipotenusa de un triángulo rectángulo es siempre mayor (o igual) que cualquiera de los catetos, la máxima velocidad permitida para una partícula es la velocidad de la luz, siempre que la partícula no tenga masa, como el fotón. Si tuviese masa, nunca podrá alcanzar la velocidad de la luz.

Este aumento de masa se puede observar en aceleradores de partículas: las colisiones entre dos protones generan muchos tipos de partículas. Si sumamos las masas de esas partículas, observamos que se supera las masas de los dos protones. Si tenemos en cuenta el aumento de la masa a las velocidades a las que chocan, los resultados cuadran.

En desintegraciones de núcleos pesados, la masa de los productos es menor a la del núcleo del que proceden. Teniendo en cuenta la energía emitida y la relación que hay entre esa energía y la masa (la famosa ecuación E = mc2), los resultados vuelven a cuadrar.

Esta serie de Relatividad Especial va llegando a su fin...en la siguiente entrada trataré la famosa "Paradoja de los Gemelos".

¡Un saludo!

Contracción Espacial

Al igual que vimos en la entrada anterior, las grandes velocidades deforman también el espacio. En La Dilatación Temporal pudimos ver cómo el tiempo se iba ralentizando a medida que nuestra velocidad, con respecto a un observador en reposo, se aproximaba a c. Siempre que nos referimos a Relatividad Especial, debemos tener en cuenta que tratamos con velocidades constantes, es decir, ausencia de aceleración. No hay ningún experimento físico que podamos realizar para determinar si nos movemos a velocidad constante o si estamos parados. Este era otro postulado de Einstein. Debido a esto, siempre que hablamos de velocidad, tenemos que referirnos respecto a qué. Y todo porque todo es relativo, excepto la velocidad de la luz.

Volviendo al tema que hoy nos concierne, vamos a ver por qué la longitud se contrae:

Supongamos que María tiene un láser con el que apunta a un espejo. Como María sabe cuál es la velocidad de la luz, y además tiene un cronómetro muy preciso, puede calcular la distancia entre ella y el espejo. Ahora imaginemos que Juan se mueve hacia María en la misma dirección que la recta que une a María y al espejo, a una velocidad muy próxima a la de la luz. Él también puede medir la distancia entre María y el espejo, porque posee un cronómetro...pero debemos recordar que en su cronómetro, debido a la velocidad, el tiempo transcurre más lento que en el de María. Te recomiendo leer la entrada anterior para refrescar tu memoria (puedes leerla aquí). Como la velocidad de la luz es la misma para todo observador, y dado que va a cronometrar más tiempo que María, el espacio necesariamente debe de ser menor.

Si Juan se aproximase a María a una velocidad v = 0,87c, y para María el tiempo que tarda el rayo de luz en alcanzar el objeto es t = 1s, para Juan ese tiempo aumentaría hasta 2s. Como consecuente, y para cumplir la igualdad de c = e/t, la distancia entre María y el espejo (teniendo en cuenta que la luz tiene que ir y volver) sería de 150.000 km. Como Juan mide el doble de tiempo, es lógico pensar que la distancia debe de ser la mitad, precisamente 75.000 km.

Otro modo de verlo es como una consecuencia directa de la dilatación temporal. En la expresión c = e/t (donde c es la velocidad de la luz, y por tanto constante, e es el espacio recorrido por una onda lumínica, y t es el tiempo empleado) podemos ver que si aumentamos el tiempo (dilatación temporal), es necesario que disminuyamos el espacio recorrido (contracción espacial)...y todo esto gracias a que sabemos la constancia de c.

Ahora, igual que hicimos con la dilatación temporal, vamos a intentar deducir la fórmula de la contracción espacial:

Supongamos que nos encontramos en una habitación como la de la imagen inferior, sin ventanas y sin saber si nos movemos a velocidad constante o si estamos parados. En un instante t'1, desde una de las paredes se emite una onda en dirección a la otra pared a la velocidad de la luz, c. Esta onda se recibe en la pared de enfrente en el instante t'2.

Para calcular la longitud de esa habitación, L', multiplicamos el tiempo que emplea la onda en llegar por su velocidad, tal y como hacemos en la imagen inferior.

Ahora supongamos que nos encontramos fuera de la habitación, que además es transparente y podemos ver en su interior. Ahora sabemos que se mueve con una velocidad constante v. En la posición x1 (instante t1) se emite la misma onda que antes, que choca con la otra pared en el punto x2 (instante t2):

El espacio recorrido por esa onda, tal y como vemos en la imagen, será:

Pero resulta que ese espacio es también la velocidad a la que se mueve la onda multiplicada por el tiempo que emplea, dicho de otro modo:

Y ese espacio, finalmente, es igual al incremento de longitud en el eje x:

Igualando las expresiones anteriores tenemos que:

Despejamos L:

Recordamos el factor ß y las transformaciones de Lorentz para longitud y tiempo:

Sustituimos en la fórmula que habíamos obtenido el tiempo y el espacio teniendo en cuenta las transformaciones de la imagen superior:

Teniendo en cuenta que el incremento de x' es igual a L'

Obtenemos la fórmula que relaciona el espacio medido por un observador en reposo L' con el medido por un observador en movimiento relativo L.

Como ß tiende a 0, cuando nos aproximamos a la velocidad de la luz, las longitudes tienden a achatarse. Para un fotón (partícula constituyente de la luz y que se mueve a c), el Universo no tiene ninguna dimensión, ni espacial (porque su factor ß = 0, y por consiguiente las longitudes son nulas), ni temporal (por lo mismo). Un fotón está congelado en el tiempo, y si pudiese pensar, no notaría que tardase tiempo alguno en recorrer el espacio, porque este no tendría volumen.

Si te ha gustado, comenta y comparte. Nos vemos la próxima semana con "El aumento de la masa".

Dilatación Temporal

En la entrada anterior comencé una serie dedicada a la Relatividad Especial. Puedes leerla aquí: Introducción. En ella expliqué los antecedentes de la teoría, centrándome en el experimento de Milchelson y Morley, en el que demostraron que la velocidad de la luz en el vacío, c, era constante. Esta afirmación la introdujo Einstein en sus postulados, de la que deduciremos fenómenos sorprendentes. Hoy nos centraremos en cómo cambia la percepción del tiempo para dos observadores que se mueven a velocidades distintas.

A quien mucho le debemos en el mundo de la física es a H. A. Lorentz. Lo que nos incumbe hoy son sus transformaciones, ecuaciones matemáticas que relacionan el espacio y el tiempo dependiendo de la velocidad. A partir de ellas, deducimos que el tiempo se relantiza a medida que nos movemos más y más rápido, según esta ecuación simplificada:

t' = t·ß, donde ß es un factor que disminuye con la velocidad, t es el tiempo que mide el observador que está en reposo y t' el tiempo que mide el observador en movimiento.

Si quieres la dmostración de esta fórmula de manera sencilla, clic aquí.

A velocidades cotidianas (andar, correr, un coche, un avión o incluso una nave espacial), ß vale 1 o muy próximo a 1, conque el tiempo para una persona en reposo y otra dentro, por ejemplo, de un coche, es el mismo. Pero a medida que nos aproximamos a c, ß cada vez vale menos, tendiendo a 0. De aquí se deduce, por ejemplo, que mientras para una persona en la Tierra pasan 10 años, para una persona que hipotéticamente se moviese a un 87% de la velocidad de la luz, pasarían 5 años. Obviamente, esto es una forma de viajar en el tiempo hacia el futuro, más rápido de lo que lo estamos haciendo ahora, segundo a segundo. Para el viajero, el experimento de moverse tan rápido supondría un viaje en el tiempo hacia el futuro.

Pero, ¿cómo podemos entender esto fuera de las matemáticas?

Imagina que tenemos dos relojes formados cada uno por dos espejos uno enfrente del otro, tal y como muestra la imagen superior. Entre ellos hay un fotón que se mueve a la velocidad de la luz, rebotando de uno a otro. Cada vez que rebota, suena un "tic" que nos permite medir el tiempo. 

Si movemos uno de los dos relojes de izquierda a derecha, como en la figura superior, el fotón tardará más en alcanzar el espejo, porque como hemos dicho, no se puede superar la velocidad de la luz. El tiempo que tarde en rebotar dependerá de la velocidad a la que se mueva el reloj, ya que c es constante. Un reloj en reposo y otro en movimiento marcan tiempos diferentes. Lo entenderemos mejor en el siguiente vídeo:

Documental completo aquí.

Ahora traduciremos esto a lo que ocurriría en nuestro cuerpo o en cualquier objeto a esas velocidades: las interacciones electromagnéticas entre nuestros átomos, al igual que gran variedad de fenómenos, suceden a la velocidad de la luz. A grandes velocidades, estos procesos se ralentizarían tal y como hemos visto en el vídeo, lo que supondría esa dilatación temporal.

Si por algún casual pudiésemos viajar a la velocidad de la luz, algo imposible como veremos en entradas sucesivas, el fotón de nuestro reloj nunca alcanzaría el otro espejo porque se alejaría de él a su misma velocidad. De este modo, cualquier persona parada que nos observase nos vería congelados en el tiempo, al igual que para nosotros, él sería el que estaría "congelado".

La dilatación del tiempo se ha medido y demostrado experimentalmente. Se ha comprobado el retraso que sufren algunos relojes atómicos durante un viaje en avión respecto a otros que han permanecido quietos. La diferencia temporal es de pocos nanosegundos debido a la escasa velocidad de un avión en escalas relativistas.

Otro ejemplo es la desintegración de muones relativistas. Un muón es una partícula subatómica de la familia de los leptones, al igual que el electrón, con una carga negativa pero más masa que el electrón. Se desintegra en dos microsegundos, produciéndose un electrón y dos neutrinos. En grandes aceleradores de partículas como el LHC, donde consiguen acelerar muones a velocidades próximas a c, se ha comprobado que la vida media de estas partículas aumenta. Este fenómeno se puede explicar mediante la dilatación temporal que sufren a esas velocidades.

Otro dato sobre los muones: podemos detectar muones que nos llegan de capas altas de la atmósfera, pero con esa vida media no deberían recorrer ni un kilómetro...la única explicación razonable es esa dilatación temporal que sufren a esa enorme velocidad, que les aumenta la vida media y consiguen recorrer más espacio (que a su vez se contrae, como ya veremos).

Ahora bien, Antonio y Juan son dos gemelos. A la edad de 20 años, Antonio se embarca a bordo de una travesía espacial a un 95% de la velocidad de la luz. Medido en años terrestres, el viaje dura 60 años. Para Juan, su hermano en la nave viaja tan rápido que el tiempo deberá transcurrir para él más lento. De este modo, al volver, Antonio regresaría con 39 años mientras que Juan tendría 80. Pero para Antonio, que se encuentra en reposo en su nave, el que parece que se aleja de él es Juan, y al reencontrarse el anciano debería ser él y no su hermano, al contrario que antes. Solo uno tiene razón, ¿pero cuál?

Esta es la famosa paradoja de los gemelos, que dentro de dos entradas analizaremos y resolveremos, para ver quién de los dos tiene razón.

Y hasta aquí la entrada de hoy. Si te interesa la deducción matemática de la fórmula de la dilatación temporal, te animo a que sigas leyendo. En la próxima entrada trataré la contracción del espacio.

Las matemáticas de la dilatación temporal

Partiremos de las transformaciones de Lorentz tomándolas como verdaderas, de donde deduciremos la fórmula antes mencionada de la dilatación temporal.

Esta es la transformación de Lorentz que relaciona el tiempo en movimiento t' con el tiempo en reposo t.

El factor ß se calcula así: (c es la velocidad de la luz en el vacío y v es la velocidad del cuerpo en movimiento, que es constante)

Sustituímos ß en la ecuación de Lorentz:

El cuerpo en el eje cartesiano se desplaza a velocidad constante v:

Relación entre velocidad, espacio y tiempo: 

Sustituimos x en la ecuación de Lorentz y despejamos:

Hasta aquí hemos deducido la dilatación temporal t' = t·ß

En la imagen inferior deducimos que "en cada segundo, medido desde el sistema en reposo, el tiempo se retrasa (1-ß) segundos"

Espero que hayáis disfrutado con esta entrada, ya que yo lo he hecho escribiéndola. Dejad sugerencias y comentarios, y nos vemos en unos días con "La contracción del espacio".