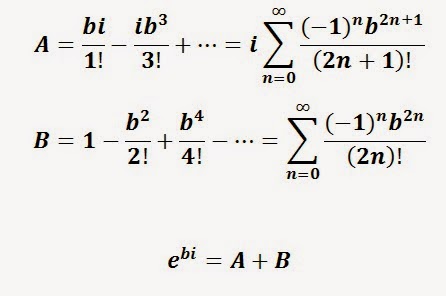¿Existen los números?

Desde pequeños hemos aprendido que los naturales son el 0, el 1, el 2,... y que hay infinitos. Sabemos que si vamos sumando 1 a cada número obtenemos el siguiente, y que da lo mismo hacer 2+5 que 5+2; en ambos casos obtendremos 7. ¿Pero son estos resultados algo trivial? En absoluto.

¿Cómo podemos estar seguros de que existen los números? ¿Cómo sabemos que 1+1 = 2? Estas preguntas se las hizo el matemático Giuseppe Peano en el siglo XIX, introduciendo los conocidos como Axiomas de Peano. Tratemos de introducirlos partiendo de muy pocos preceptos evidentes e indubitables.

Supongamos que existen entes que llamaremos "conjuntos", y que contiene otros entes llamados "elementos". Digamos que dos conjuntos $A$ y $B$ son iguales si cada uno está incluído en el otro, es decir, $A=B\leftrightarrow A\subset B\wedge B\subset A$. Éste es el axioma de extensión. Nos creeremos que para todo conjunto $A$ y condición $T$ existe $B\subset A$ definido como los elementos de $A$ que verifican $T$. Éste es el axioma de especificación. Ahora soy capaz de demostrar que existe el cero: definiendo $B=\{x\in A:x\neq x\}$ me doy cuenta de que este conjunto no posee elementos. Lo llamaré conjunto vacío o cero, denotándolo como $\Phi$. Bautizaré al cero como 0, al $\{0\}$ lo llamaré uno, al $\{0,1\}$ lo llamaré dos,...

Axioma de la unión: dada una colección de conjuntos $C$, existe uno que contiene a todos los elementos de al menos uno de ellos, I mean, $\exists V:\forall A\in C\wedge\forall x\in A$ se tiene que $x\in V$. El conjunto unión se denotará como

$\bigsqcup_{A\in C} A=\{x\in V:x\in A\}$

Definiremos también el sucesor de $A$ como $A+=A\cup\{A\}$ y el concepto de conjunto sucesor, sobre el que pivota la teoría de Peano. $S$ es un conjunto sucesor si $0\in S$ y si $A\in S\Rightarrow A+\in S$. Tomaremos como axioma la existencia de un conjunto sucesor. A partir de unión y especificación construímos el conjunto intersección:

$\bigcap_{A\in C} A=\{x\in \bigsqcup_{A\in C} A:x\in A\forall A\in C\}$

 Lema: si $A$ y $B$ son conjuntos sucesores, $A\cap B$ también lo es. Es evidente pues si $0\in A\wedge 0\in B\Rightarrow 0\in A\cap B$ y además si $n\in A\wedge n\in B\Rightarrow n+\in A\cap B$ pues $n+\in A\wedge n+\in B$ por hipótesis. Como corolario podemos afirmar que dada una colección de conjuntos $D$ y un conjunto $A$, $\bigcap_{A\in C} A$ es un conjunto de sucesores al que llamaremos conjunto de los número naturales: $\mathbb{N}=\bigcap_{A\in C} A$. Ahora estamos en disposición de enunciar los axiomas de Peano.

Propiedades de $\mathbb{N}$

1. Si $S\subset\mathbb{N}$ es sucesor entonces $S=\mathbb{N}$, pues $0\in S$ y toda vez que $n\in S$ entonces $n+\in S$. Esta es una generalización del principio de inducción. Otra forma de probarlo es mediante el Principio del Máximo: dado un conjunto acotado superiormente, éste tiene un máximo.

2. Cada $n\in\mathbb{N}$ satisface que $n+\neq 0$ pues $n\in n+$ y por tanto no puede ser $n+=\Phi$.

3. Dados $n,m\in\mathbb{N}$ con $n+=m+$ entonces $n=m$. Es una trivialidad, pues si $n=m$ no hay nada que demostrar, y si $n\neq m$ entonces como $n\cup\{n\}=m\cup\{m\}\rightarrow n\in m\rightarrow n\subset m$ y por la misma razón $m\subset n$ luego por el exioma de extensión $n=m$.

Considerando el 1 en vez del 0 se tiene:

Axiomas de Peano

(1) $1\in\mathbb{N}$ o más formal, $N(1)$.

(2) Si $n\in\mathbb{N}\rightarrow n+\in\mathbb{N}$ ó $\forall x(N(x)\rightarrow N(x'))$

(3) $\forall n\in\mathbb{N}, n+\neq 1$ ó $\neg \ \exists \ x(N(x)\wedge x'=1)$

(4)  Si $1\in S\wedge n\in S\rightarrow n+\in S$ entonces $S=\mathbb{N}$. Otra forma más elegante es $(\phi(1)\wedge\forall x(\phi(x)\rightarrow\phi(x')))\rightarrow\forall x\phi(x)$

(5) Dados $n,m\in\mathbb{N}$ con $n+=m+$ entonces $n=m$. Formalmente, $\forall x\forall y((N(x)\wedge N(y)\wedge x'=y')\rightarrow x=y)$

$N(n)$ simboliza que $n\in\mathbb{N}$. x' denota al sucesor de x. $\phi$ es cualquier proposición sobre $\mathbb{N}$.

Hemos visto que tan solo con unos pocos axiomas razonables y reglas lógicas hemos demostrado que existe un conjunto al que llamamos "números naturales" que verifica una serie de propiedades mencionadas y otras que no hemos citado, pues no son relevantes para el tema a tratar. Ahora bien, ¿qué operaciones podemos hacer con los números y qué propiedades cumplen? Para ello tendremos que definir un par de conceptos más y ver el Teorema de Recurrencia:

Sea $a\in X$ y $f:X\rightarrow X$. Existe una única función $u:\mathbb{N}\rightarrow X$ tal que $u(0)=a$ y $u(n+)=f(u(n))$ $\forall n\in\mathbb{N}$.

Demostración:  Sea $C=\{A\subset\mathbb{N}\times X:(0,a)\in A\wedge (n+,f(x))\in A \ \text{siempre que} \ (n,x)\in A\}$. Probaremos en primer lugar que $u:=\bigcap_{A\in C} A\in C$. En efecto, si $(n,x)\in u\Rightarrow (n,x)\in A \ \forall A\in C\Rightarrow (n+,f(x))\in u$, y además como $(0,a)\in A \ \forall A\in C$, entonces $(0,a)\in u$, luego $u\in C$. Si ahora probamos que $u$ es función, acabaría la demostración, es decir, que para cada $n\in\mathbb{N}$ existe un solo $x\in X$ tal que $(n,x)\in u$. Como siempre, invoquemos a un conjunto sucesor. Sea $S=\{n\in\mathbb{N}:\exists \ \text{como mucho un } x\in X:(n,x)\in u\}$. Evidentemente $0\in S$. Supongamos que $n\in S$, entonces $(n,x)\in u$ y por cómo está definida $u$ se llega claramente a que $n+\in S$, luego $S=\mathbb{N}$ y quedaría probado el Teorema. El detalle de "como mucho un $x\in X$" se demuestra por reducción al absurdo suponiendo que hay dos y llegándose a que son el mismo. En efecto sea $V=u/\{(0,b)\}$ y $(n,x)\in V$. Entonces por Peano, $(n+,f(x))\in u$ y como $n+\neq 0\forall n\in\mathbb{N}$ entonces $(n+,f(x))\in V\Rightarrow V\in C\wedge u\subset V$ contra la hipótesis.

Sea ahora $s:\mathbb{N}\rightarrow\mathbb{N}$ definida por $s(n)=n+$. El Teorema anterior nos garantiza la existencia de una función $S_m:\mathbb{N}\rightarrow\mathbb{N}$ tal que $S_m(0)=m$ y $S_m(n+)=s(S_m(n))$. Llamaremos a esta función la suma, denotándola como $S_m(n)=m+n$. Por ejemplo, $1+1=S_1(1)=S_1(0+)=s(S_1(0))=s(1)=1+=2$. Nunca una operación tan sencilla se hizo con tanta elegancia. La función así definida es única, luego podemos estar tranquilos: 1 y 1 siempre sumarán 2.

De esta definición se pueden deducir las propiedades que desde que íbamos a la escuela conocemos: la propiedad asociativa, distributiva y la existencia del 0 como elemento neutro. Pese a ser repetitivos, las demostraremos:

El 0 como elemento neutro

Queremos probar que $0+m=m+0=m$ $\forall m\in\mathbb{N}$. Es evidente que $m+0=S_m(0)=m$, luego bastará probar que $0+m=m$. Sea $S=\{m\in\mathbb{N}:0+m=m\}$. Se ve que $0\in S$ y que si $m\in S\Rightarrow m+\in S$ ya que $0+m+=S_0(m+)=s(S_0(m))=(0+m)+=m+$, luego $\mathbb{N}=S$ y queda probado.

Propiedad conmutativa

Sea $S=\{a\in\mathbb{N}:a+b=b+a \ \text{con} \ b\in\mathbb{N}\}$. $0\in S$ pues es neutro. Si $n\in S$ entonces $b+n+=S_b(n+)=s(S_b(n))=s(b+n)=s(n+b)=(n+b)+=n+ +b\Rightarrow n+\in S$, por lo que también queda probada.

Propiedad asociativa

Definiendo un conjunto $S$ como en los casos anteriores y demostrando que es sucesor se deduce trivialmente. No queremos ni atosigar al lector ni insultar a su inteligencia.


Por el T. de la Recurrencia podemos definir $P_m:\mathbb{N}\rightarrow\mathbb{N}$ con $P_m(0)=0$ y $P_m(n+)=S_m(P_m(n))$. Esta función se llamará producto y se denotará como $P_m(n)=m\times n$. Por ejemplo, $1\times 2=P_1(2)=P_1(1+)=S_1(P_1(1))=S_1(1)=2$. Al igual que antes podemos verificar las propiedades asociativa y conmutativa, demostrar que el 1 es el elemento neutro y demás, cosas que dejaremos como ejercicio al lector. Para hacerlo basta encontrar un conjunto sucesor, como hicimos antes.

Podemos definir otras operaciones como la potencia. En este caso, de nuevo, $E_m:\mathbb{N}\rightarrow\mathbb{N}$, $E_m(0)=1$, $E_m(n+)=P_m(E_m(n))$ y se denota por $E_m(n)=m^n$. Al igual que antes, podemos demostrar todas las propiedades que ya sabemos sobre las potencias, pero ahora de una forma más elegante y rigurosa. Por ejemplo:

$E_m(n+k)=E_m(n)\times E_m(k)$

Demostración: sea $S=\{n\in\mathbb{N}:E_m(n+k)=E_m(n)\times E_m(k)\}$. Es evidente que $0\in S$. Supóngase que $n\in S$. Entonces

$E_m(n++k)=E_m((k+n)+)=P_m(E_m(k+n))=P_m(E_m(n)\times E_m(k))=$

$=m\times E_m(n)\times E_m(k)=E_m(n+)\times E_m(k)$

suponiendo demostrada la propiedad asociativa del producto.


Espero que esta entrada, pese a quizá ser demasiado formal, os haya gustado.

Un saludo!

La Igualdad de Euler

Leonhard Euler fue un matemático y físico suizo que vivió en el siglo XVIII. Es considerado uno de los grandes genios de la historia de la Ciencia. A él le debemos la existencia del número que lleva su nombre, el número e. Si quisiésemos hablar de todo lo que hizo, esta entrada se haría interminable, por lo que hoy me centraré en la famosa Ecuación de Euler:

Vamos a intentar demostrar esta identidad de gran belleza a partir de las Series de Taylor y Maclaurin, que son representaciones de una función (como el seno, el coseno o una exponencial) a partir de la suma de infinitos términos. Por ejemplo: sen 45º se puede escribir como la suma de infinitos sumandos que converge hacia el valor concreto del sen 45º. Las series que necesitaremos son las siguientes:

También necesitaremos algo de números complejos. Recordemos que un número complejo z puede escribirse como z = a + bi, siendo i la unidad imaginaria (raiz cuadrada de -1). Podemos escribir lo siguiente:

Ahora intentemos escribirlo mediante las Series de Taylor:

Podemos observar que hay algunos términos que poseen la unidad imaginaria i, pero otros no. Vamos a llamar A a la suma de los términos que incluyen i, y B a la suma de los que no:

Siendo un poco observadores, podemos escribir lo siguiente:

Ahora vamos a igualar b al número pi:

Con lo que queda demostrada la Identidad de Euler, dotada de una belleza espectacular y de misterio. Relaciona los cinco números básicos de las Matemáticas de una forma asombrosamente básica.

No sabemos cuál es su significado, pero sabemos que es verdad: una verdad eterna y bella, por lo que muchos la consideran la igualdad más importante de las Matemáticas.

Podemos tomar logaritmo neperiano a ambos lados y observar cuánto vale el logaritmo neperiano de -1:

Si os ha gustado la entrada matemática de hoy, os invito a comentar y compartirla. 

Un saludo, nos vemos en la próxima!

Resolviendo la paradoja de Aquiles y la tortuga

Zenón de Elea fue un filósofo griego muy conocido por plantear numerosas paradojas relacionadas con el movimiento. De entre todas ellas, la más famosa puede que sea la de Aquiles y la tortuga. 

Aquiles decide echar una carrera a una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.

Todos sabemos que Aquiles ganará de sobra la carrera, igual que pensaba Zenón. Zenón planteó 40 paradojas de este estilo, debatiendo sobre el espacio, el tiempo y el movimiento. Proponía estos ejercicios mentales para reducir al absurdo las teorías de que la suma de infinitos números tenga que dar infinito. 

Si la suma de infinitos sumandos siempre fuese igual a infinito, Aquiles nunca ganará la carrera, pero esto matemáticamente y físicamente no es así. 

Supongamos que la velocidad de la tortuga es de 1 m/s, la velocidad de Aquiles es de 10 m/s y la ventaja inicial es de 100 m. En solo 10 segundos, Aquiles habrá alcanzado el punto desde el que sale la tortuga, y esta habrá avanzado 10 metros más. Esos 10 metros los recorre Aquiles en 1 segundo, pero la tortuga habrá avanzado 0,1 metros más...y así sucesivamente. Lo que plantea la paradoja es que 10 + 1 + 0,1 + ... da como resultado infinito, pero eso es incorrecto.

Cada vez, Aquiles tarda 10 veces menos en recorrer el trozo que lo separa de la tortuga. Esta fórmula nos puede ayudar a conocer todos los tiempos empleados (progresión geométrica decreciente):

Sucesión de tiempos empleados
expresada en segundos

Aplicando una fórmula que no vamos a demostrar ahora (fórmula de la suma de los infinitos términos de una progresión geométrica decreciente), podemos hallar la suma de esos tiempos. La demostración se realizaría restando a la suma de todos los términos, la suma multiplicada por la razón, pero por comodidad no lo vamos a hacer.

Como vemos en la imagen superior, la suma de 10 + 1 + 0,1...da como resultado 11,1 segundos. Aunque haya infinitos sumandos, el resultado es finito. Esto demuestra que Aquiles alcanza a la tortuga y lógicamente gana la carrera.

Podemos resolverlo también utilizando las leyes del movimiento, ya que conocemos las velocidades de ambos corredores la diferencia de posiciones. Igualando las posiciones conseguimos despejar el tiempo transcurrido en cruzarse.

Por lo tanto, una suma de infinitos términos decrecientes puede dar un resultado finito, como en este caso.

Un saludo, nos vemos en la próxima. No os olvidéis de compartir esta entrada!

Cinemática y Gravitación

¿De qué depende el tiempo que tarda en caer un objeto en caída libre?

Como es lógico, de la altura. ¿Pero y la aceleración? ¿Es constante siempre? La respuesta es que no.

Esa aceleración se debe una fuerza de carácter gravitatorio, que a su vez depende de la distancia entre los cuerpos y sus masas (Ley de la Gravitación Universal). Como la fuerza aumenta conforme al objeto se acerque a la Tierra, también lo hará la aceleración para una masa m constante. Por esto, he decidido combinar las ecuaciones de cinemática con las de gravitación, para obtener unas nuevas que relacionen el tiempo de caída con la altura (teniendo en cuenta una aceleración variable). 

Esto quiere decir que la aceleración que sufre nuestro objeto depende de la altura, y nuestro objetivo será hallar la aceleración media entre el momento en el que está arriba del todo y el momento en el que toca el suelo. Recordemos las constantes con las que vamos a trabajar:

Si graficamos la aceleración en función de la altura, obtenemos una gráfica del siguiente tipo: (función potencial de exponente entero negativo par)

Cuando la altura vale 0, se obtiene el conocido valor de 9,8 m/s2 para la aceleración. A medida que la altura aumenta, este valor tiende a 0 en el infinito. Podemos observar que debajo de la función se forma un área:

Este área (A) corresponde geométricamente con la integral definida en el intervalo [0, h] de la función aceleración. Recordemos que la aceleración es la derivada de la velocidad con respecto al tiempo, entonces la integral indefinida de la función aceleración (diferencial de tiempo) corresponde con la función velocidad, que depende del tiempo con una aceleración constante. Podemos decir entonces que el área A se corresponde con la aceleración multiplicada por el tiempo. Podemos hallar la aceleración media así:

Esta nueva función tiene aceleración constante, y el área (A) de debajo en el intervalo [0, h] es la misma. Por eso podemos decir que la aceleración media se corresponde con ese área dividida entre h. Viéndolo como si fuese un rectángulo, el área A sería igual a la base h por la altura am.

Vamos a comparar las ecuaciones obtenidas con las ecuaciones "normales" donde consideramos la aceleración, g, constante:

Graficando las dos ecuaciones del tiempo con respecto a la altura obtenemos lo siguiente:

La altura (h) está representada en el eje de abscisas en km, y el tiempo (t) está representado en el eje de ordenadas en segundos. La línea negra es la fórmula con aceleración constante, y la línea roja es la que hemos hallado, donde la aceleración es variable.

Podemos observar que a alturas "pequeñas" las dos funciones están casi superpuestas. A partir de 300 o 400 km ya se observan diferencias que se van acrecentando con el tiempo. Para que nos hagamos una idea, la altura desde donde se lanzó Felix Baumgartner está representada por la línea azul, es decir, la diferencia de tiempos no alcanzaba ni 1 segundo.

Si representamos la altura de un objeto en función del tiempo que tarda en caer según las dos fórmulas:

De nuevo, la línea roja será la que hemos hallado en esta entrada y la negra la que considera la aceleración constante. A alturas bajas, hasta los 300 km, la diferencia es insignificante. A partir de esa altura, es un factor a tener en cuenta. Una altura de 200 km representa tan solo el 3% del radio terrestre.

Finalizaré la entrada recordando las dos ecuaciones que hemos hallado hoy, la que relaciona la altura (h) con respecto al tiempo y la que relaciona el tiempo (t) con respecto a la altura desde la que se lanza un cuerpo en caída libre:

Nota: considero todos los tiempos, lógicamente, como positivos si no pongo el símbolo "+" delante de las raíces.

Estas ecuaciones se pueden aplicar en otros planetas, sustituyeno el radio y la masa por el que corresponda. Es necesario decir también que en estas ecuaciones omitimos por completo el rozamiento con el aire, que es un factor muy a tener en cuenta. Los tiempos que hallemos con estas fórmulas serán ligeramente superiores a los experimentales por este motivo. Posteriormente ampliaré las ecuaciones teniendo en cuenta esos datos.

Hasta dentro de unos días con otra entrada. Espero que os haya gustado esta, ya que le he dedicado bastante tiempo entre obtener las ecuaciones y preparar la entrada y las gráficas.

Un saludo!

Paradoja de los Gemelos

Y finalmente llegamos al final de esta serie dedicada especialmente a Relatividad Especial. Si quieres leer el resto de entradas sobre este tema, te invito a que hagas clic en el siguiente enlace, donde están todas agrupadas: Serie de Relatividad Especial.

Hoy vamos a tratar la Paradoja de los Gemelos. Antes de todo, veamos en qué consiste:

"Dos hermanos gemelos deciden hacer un peculiar experimento: uno de ellos es astronauta, y se embarca en un viaje espacial a velocidades próximas a la de la luz. Para el que permaneció en la Tierra, el astronauta ha sido el que se ha movido, por tanto al regresar habrá envejecido menos que él (de acuerdo con la dilatación temporal que sufre a esas velocidades). Pero para el astronauta, el que se ha movido respecto a él ha sido el resto del Universo...por tanto al volver, el que menos habrá envejecido habrá sido el que permaneció aquí".

Aquí reside la paradoja, ya que lo que miden los dos no tiene sentido en el momento en el que se encuentran. Si analizamos a fondo el experimento, veremos qué gemelo tiene razón. ¿Te apuntas?

Antes de nada, recordemos que a grandes velocidades el tiempo se ralentiza, el espacio se contrae y la masa aumenta. Vamos a observar el experimento desde el punto de referencia del gemelo astronauta primero, y finalmente el otro gemelo. De este modo queremos saber qué ocurre exactamente y cuál de los dos envejece más. Vamos a añadir un matiz: tanto el astronauta como su hermano tienen una linterna con la que envían un destello cada segundo a su hermano.

El astronauta decide embarcarse en su travesía espacial de 10 años luz a 261.000 km/s (he escogido este valor para simplificar las cuentas al final). El astronauta no mide 10 años luz, sino que debido a la contracción espacial que experimenta, para él el trayecto es de 5 años luz. A la velocidad que lleva, debería tardar 11,5 años ida y vuelta en completar el trayecto. Sin embargo, para el que permanece en la Tierra no es así...

Aunque el hermano que se queda en la Tierra encienda y apague su linterna cada segundo, el astronauta no ve esos destellos cada segundo, porque cada segundo la luz tiene que recorrer una distancia de 261.000 km más (el espacio que recorre su nave en un segundo). Debido a esto, los destellos se ralentizan cada 1,87 segundos...y si aplicamos la fórmula de dilatación temporal...los destellos se producirán cada 3,74 segundos.

Hemos dicho que para el astronauta, el tiempo de ida y vuelta son 11,5 años, entonces en ir emplearía la mitad, un total de 5,75 años. Como el tiempo en la Tierra transcurre 3,74 veces más lento, el tiempo que habrá medido el hermano de la Tierra será 5,75/3,74...es decir, 1,5 años.

Cuando el astronauta llega a su destino y se da la vuelta, el proceso se invierte. Cada segundo, la luz tiene que recorrer 261.000 km menos, lo que provoca que esos destellos los perciba cada 0,26 segundos teniendo en cuenta la dilatación temporal. Entonces, los 5,75 años de vuelta de la nave para nosotros son como 21,5 años, el resultado de dividir 5,75/0,26.

Astronauta: 5,75 + 5,75 = 11,5 años

Tierra: 1,5 + 21,5 = 23 años

Si hacemos cuentas, el astronauta ha vivido 11,5 años en total y nosotros en la Tierra hemos vivido 23 años, el doble, exactamente el mismo resultado que obtendríamos según la transformación de Lorentz.

Según la primera parte de este experimento, el que menos envejece es el astronauta.

Ahora vamos a centrarnos en el hermano que permanece en nuestro planeta. Al igual que antes, los destellos de su hermano le llegan cada 3,74 segundos. La distancia que recorre su gemelo son 10 años luz a un 87% de la velocidad de la luz, entonces la nave tarda 11,5 años "terrestres" en llegar al destino.

Cuando el astronauta llega al final de la travesía y se da la vuelta, en la Tierra vamos a seguir notando los destellos cada 3,74 segundos durante 10 años más, porque se encuentra a 10 años luz de nosotros. Eso quiere decir que pasamos un total de 21,5 años percibiendo los destellos, lo que para el astronauta serían 5,7 años.

Como el viaje de vuelta dura 11,5 años (10 años luz a 261.000 km/s), y 10 de esos años los percibimos cada 3,74 segundos, quedan 1,5 años. A partir de ese momento, desde la Tierra comenzamos a percibir los destellos aceleradamente, porque ya ha llegado el último que se emitió desde el punto más lejano a 10 años luz. Durante esos 1,5 años, los destellos se producen cada 0,26 segundos. Eso quiere decir que para el tripulante de la nave, ese año y medio equivale a 1,5/0,26 = 5,7 años.

Astronauta: 5,7 + 5,7 = 11,5 años

Tierra: 11,5 + 10 + 1,5 = 23 años

Si echamos cuentas, el astronauta ha vivido 11,5 años y en la Tierra han pasado 23 años. Exactamente el mismo resultado que en el caso anterior. Aquí queda resuelta la paradoja.

El gemelo que envejece menos es el astronauta.

En ambos casos se cumple que el que menos envejece es el astronauta, tal y como predicen las ecuaciones de Lorentz y Einstein.

No hemos tenido en cuenta la dilatación temporal producida por la gravedad, que también afectaría al experimento. El gemelo de la Tierra se encuentra en un sistema acelerado constante (la aceleración de la gravedad sería g = 8,81 m/s2), pero el astronauta también tendría que acelerar para lograr tales velocidades, por lo que los datos del experimento podrían variar teniendo en cuenta estas consideraciones.

Aquí llegamos al final de la serie dedicada a Relatividad Especial. Espero que os haya gustado, y como ya sabéis, aquí abajo podéis dejar comentarios.

¡Un abrazo científico!

¡La Luna a 40 pasos!

¿Cuántas veces tenemos que doblar un folio para llegar a la Luna? La respuesta resultará increíble: 42.

Veremos ahora el porqué:

Un taco de 500 folios tiene un grosor de 5 cm aproximadamente. Si dividimos el grosor entre el número de folios, obtenemos que cada folio tiene un grosor de tan solo 0,1 mm.

Si doblamos por la mitad el folio, su grosor será el doble (0,2 mm); la segunda vez ya será 0,4 mm; la siguiente, 0,8 mm...y así sucesivamente, duplicándose el grosor en cada doblez:

Folio original: 0,1 mm

1ª Doblez: 0,1 · 2 mm

2ª Doblez: 0,1 · 2 · 2 mm

3ª Doblez: 0,1 · 2 · 2 · 2 mm

Así, cada vez que doblamos, multiplicamos por dos el grosor. En la doblez 10, el grosor será 2^10 veces mayor. Si observamos la siguiente tabla y su correspondiente gráfica, observamos cómo crece el grosor con respecto al número de veces que doblamos el folio:

Tabla de valores

Gráfica de la función

Nos encontramos ante un crecimiento exponencial. Aunque al principio el grosor aumente poco, a mediada que seguimos doblando aumenta muchísimo. Cuando lo doblamos x veces, su grosor será 2^x veces mayor.

La distancia media entre la Tierra y la Luna es de 384.400 Km. Ahora intentaremos expresar todo esto de forma matemática, sin olvidar de indicar todo en las mismas unidades. Igualaremos el grosor de la doblez nº X a la distancia entre la Tierra y la Luna, para así despejar la X y saber cuántas veces hay que doblar el papel.

Aplico el Cambio de Base para poder realizar la operación con mi calculadora.

Es decir, doblando un folio tan solo 42 veces...¡PODEMOS LLEGAR A LA LUNA!

Matemáticamente esto queda muy bonito, pero físicamente dudo que puedas llegar a doblar el folio más de 7 u 8 veces. Si se pudiese hacer, la superficie del folio sería muy inferior, exactamente 2^42 veces más pequeña. Es como si tuviésemos una superficie cuadrada de 1200 átomos de lado (unos pocos nanómetros cuadrados)...algo que a simple vista es imposible contemplar.

Aplicando los mismos pasos, y conociendo la distancia al Sol (149.600.000 Km) tenemos que el número de veces que necesitamos doblar un folio es aproximadamente 50 (50,4 exactamente).

¡Para llegar al Sol, solo tendríamos que doblar el folio 8 veces más!

Y más sorprendente aún, mediante el mismo procedimiento solo tendríamos que doblar un folio 81 veces para llegar al centro de la Galaxia...y solamente dos veces más para llegar de punta a punta de ella...¡INCREÍBLE!

Intentad doblar un folio 42 veces y dejáis en los comentarios qué tal vuestro paseo lunar. Dejad también en los comentarios temas para mi siguiente entrada que intentaré publicar este fin de semana. Tengo pensado preparar algo chulo sobre Relatividad, pero lo dejaré para dentro de una o dos semanas, así que proponed ideas.

Un Saludo Científicos,

HASTA OTRA!