Cien años de...Relatividad General

 

BIOGRAFÍA

Aunque el título parezca una novela de Gabriel García Márquez, de quien realmente vamos a hablar en la entrada de hoy es de Albert Einstein. 

Nuestra historia no comienza en Macondo, como la de Gabo, sino en la ciudad alemana de Ulm, un 14 de marzo de 1879. Sin duda aquel fue un "Buendía". En tan "premonitoria" fecha nació el pequeño Albert, hijo de Hermann Einstein y de Pauline Koch, de ascendencia judía. 

En 1894, la familia Einstein se traslada a Milán, mientras el joven Albert permanece en Munich continuando sus estudios. En 1896 comenzó a estudiar en la Eidgenossische Technische Hochschule de Zúrich, donde fue alumno del matemático Minkowski, quién más tarde otorgaría el formalismo matemático a las teorías de su alumno.

En 1902, se incorpora a la Oficina de Patentes de Berna, y al año siguiente se casa con Milerva Maric, con quien tendrá tres hijos.

1905 es considerado como el Annus mirabilis de Einstein, por ser su época de producción científica más fructífera. Publicó un gran número de artículos acerca del movimiento browniano, de la naturaleza corpuscular de la luz, de la equivalencia masa-energía y Sobre la electrodinámica de los cuerpos en movimiento (que está colgado en la sección Archivos de esta página). Aquí surgiría la idea sobre la Teoría de la Relatividad Especial, a la que año y medio atrás dediqué una serie de entradas que puedes leer aquí.

Entre 1910 y 1914, comienzan los problemas matrimoniales entre Milerva y Einstein, que acabarán separándose. En este momento, Einstein comenzará una aventura amorosa con su prima Elsa Löwenthal. Probablemente, el año en que más fama y prestigio científico obtendría, así como grandes dolores de cabeza, fue 1915. En este año, tres frentes se abrieron en torno a él: la Primera Guerra Mundial, el divorcio con Milerva y la "batalla" para completar las ecuaciones de la Relatividad General.  

Fue gracias a un viejo amigo suyo, Marcel Grossmann, quien introdujo a Einstein en el estudio de las superficies no euclídeas en el verano de 1912, que tanta importancia irían a tener en la Teoría que presentaría Einstein tres años más tarde. Fue en esa época cuando Einstein se percató de que C.F. Gauss y su pupilo B. Riemann tenían la llave que necesitaba para completar sus ecuaciones. El matemático lituano Minkowski y antiguo profesor de Albert, tendría suma importancia en este periodo geometrizando la gravedad.

David Hilbert

Entran en escena otros matemáticos como Hilbert (de quien seguro que habrás oido hablar por su Hotel Infinito). David Hilbert, paisano espacial de Kant (aunque obviamente no temporal), comenzó con el estudio y corrección de las ecuaciones de campo de Einstein en 1912, lo que no sentó nada bien al pobre Albert al no haberlo citado en sus conferencias. Se inició así una rivalidad entre el innegable talante matemático de Hilbert y el inigualable instinto físico de Einstein.

El 14 de Noviembre de 1915, Hilbert anunció que había dado con las ecuaciones de campo gravitatorio. En este momento, Einstein trató de ponerse manos a la obra concluyendo su teoría. Cuando descubrió que sus ecuaciones predecían la irregularidad en la órbita de Mercurio y que en campos gravitatorios de baja intensidad sus ecuaciones se reducían a las de Newton, Einstein sufrió una taquicardia. El 25 de noviembre de 1915, hoy hace exactamente cien años, Einstein presentó sus ecuaciones definitivas de campo ante la academia de Berlín, adelantándose a las de Hilbert (marzo de 1916). Señoras y señores, estamos ante un día histórico.

Las asperezas entre Hilbert y Einstein se limaron a partir de entonces, gracias a que Hilbert no reclamó la autoría de las ecuaciones de Einstein.

El 29 de mayo de 1919, Arthur Eddington realizó una expedición científica a la costa de Guinea para contemplar un eclipse total de Sol. Ese día se demostró experimentalmente que la Teoría de la Relatividad General de Albert Einstein era acertada, al predecir la curvatura de un rayo de luz al pasar cerca del Sol.

Arthur Eddington

En 1922, Albert Einstein recibiría el Premio Nobel de Física por su contribución al Efecto Fotoeléctrico. En 1933 se exilia a Estados Unidos donde comienza a trabajar en Princeton, donde coincidirá con otros ilustres como Gödel o von Neumann. 

Fue una persona pacifista, contrario a todo acto de violencia, como pudo comprobarse con su rechazo a la Segunda Guerra Mundial. En boca del propio Einstein, "no sé con qué armas se luchará en la Tercera Guerra Mundial, pero sí sé con cuáles lo harán en la Cuarta Guerra Mundial: palos y piedras". 

En 1952 rechazó el convertirse en presidente del Estado de Israel, y en 1955 muere en Princeton por problemas cardiacos, sin haber logrado su objetivo de unificar todas las fuerzas de la naturaleza en una sola.

 

 

TEORÍA DE LA RELATIVIDAD GENERAL

Pese a todas las ecuaciones planteadas entre 1905 y 1915 en semajante bullicio intelectual, solo las de Einstein consiguieron tal caracter "general". Pero bien, ¿qué es lo que describen tan brillantes ecuaciones?

Cuentan que un día Einstein dialogaba con un carpintero que había caído de un andamio que le dijo: "fue como flotar en el aire". Esa idea tan simple condujo a Einstein hacia una teoría: la Relatividad General. Albert pensó que una persona flotando en el espacio sentiría lo mismo que otra en caida libre, es decir, que si vendásemos los ojos a ambas, no serían capaces de distinguir ambas sensaciones. Asimismo, no es posible distinguir entre estar en reposo sobre la Tierra o estar en un ascensor espacial que acelere con una aceleración g. Esto se conoce como el principio de equivalencia.

Einstein se dio cuenta de que la fuerza gravitatoria descrita por Newton dependía de la distancia, pero años atrás demostró que aquélla era relativa según la velocidad del observador. Algo semejante ocurría con el tiempo: no se encontraba explícitamente en la famosa ecuación de Newton, lo cual violaba el postulado básico de la Relatividad (ninguna partícula con masa puede moverse a una velocidad mayor que la de la luz en el vacío). Esto implicaba que necesitaba encontrar una teoría sobre la gravedad relativista.

Fue el matemático lituano Hermann Minkowski quien despejó el camino para que las ideas de Einstein pudiesen ser expresadas un lenguaje matemático más formal. A partir del "espacio" y del "tiempo", creó el "espacio-tiempo". Ahora el tiempo es una coordenada más, matemáticamente equivalente a "anchura", "altura" y "profundidad". De este modo, el espacio-tiempo adquiere un sentido puramente geométrico.

Analogía 4D - 3D

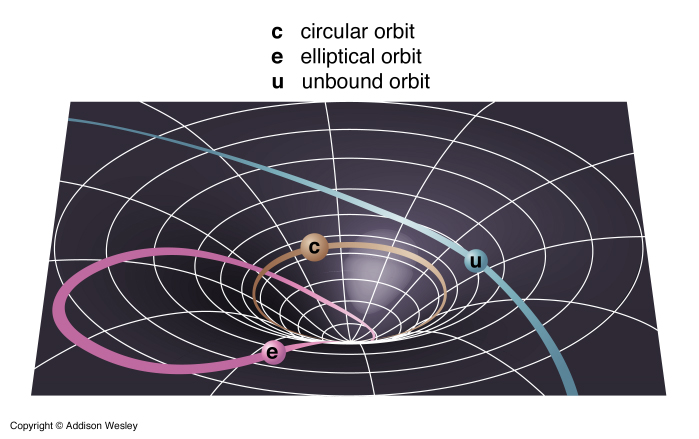
Las trayectorias de los objetos por un espacio de dimensión 3 pasan a convertirse en movimientos en 4 dimensiones denominados geodésicas. Se pueden encontrar imágenes de este tipo para ilustrar esto mismo:

 

La forma de estas trayectorias depende de la masa, es decir, la masa distorsiona el espaciotiempo. Suele ponerse el ejemplo de la bola de bolos sobre una sábana y una canica dando vueltas alrededor. La masa determina la curvatura del espacio-tiempo y ésta determina las trayectorias de los cuerpos. Esta relación viene descrita en la famosa ecuación de Einstein, el mayor logro de la mente humana para algunos.

En palabras de Wheeler, "el espacio le dice a la materia cómo debe moverse, y la materia le dice al espacio cómo debe curvarse".

CONSECUENCIAS

Es obvio que esta teoría es uno de los más magníficos constructos de la mente humana, tanto por su belleza como por sus posteriores repercusiones. Poco a poco se fue introduciendo en el resto de ramas de la Física. Quizá no hizo muy buenas migas con la Mecánica Cuántica, pero esa es otra historia.

También tuvo sus consecuencias negativas, aunque siempre por fallos humanos, no de la teoría. Con esto me refiero a las bombas atómicas de Hiroshima y Nagasaki en 1945, que nos demuestran el impacto que tuvo la ralatividad en la Física Nuclear. Absolutamente todos los efectos que predice la relatividad han sido medidos en el laboratorio: la contracción temporal, la curvatura de la luz por la presencia de un cuerpo masivo y demás. 

Actualmente, la gravedad no puede ser descrita de la misma forma que las otras tres fuerzas fundamentales. Por ello mismo se intenta comaginar las cuatro en una sola fuerza, para lo cual los físicos recurren a dimensiones más altas. Es interesante un libro de Michio Kaku titulado Hiperespacio, que puedes adquirir para ebook en mi sección Archivos. 

A Einstein y a su magnífica teoría, junto a la Mecánica Cuántica, le debemos todo el avance tecnológico del siglo XX. Sin estas teorías, no estarías leyendo este blog, al menos digitalmente. Tampoco exisiría casi ningún dispositivo electrónico, y mucho menos ordenadores, tablets, smartphones...

Otra magnífica prueba de la Relatividad General es el GPS. Para determinar la posición de tu coche, tu dispositivo GPS se "pone en hora" con cuatro satélites a la vez. De este modo, cada satélite puede determinar la distancia a la que se encuentra el dispositivo, construyendo una esfera con todos los puntos posibles en los que puede localizarse. La intersección de las respectivas cuatro esferas de cada satélite es, en efecto, un punto: tu posción. 

La sincronización entre los satélites y el GPS es vital. Teniendo en cuenta que el tiempo no transcurre a la misma velocidad para el satélite que para nosotros (por efectos gravitatorios y por la velocidad), es necesario incluir en la programación de los GPS las ecuaciones de Einstein, o si no un viaje de París a Moscú puede acabar en Roma, y no especialmente porque todos los caminos lleven a ella.

LECTURAS Y VIDEOS RECOMENDADOS

Recomiendo echar un vistazo a un famoso documental de Brian Greene que puedes ver haciendo clic aquí. Además, puedes encontrar dos de sus libros en formato digital en el siguiente enlace: Archivos. 

Muchos autores de divulgación como Michio Kaku o Stephen Hawking explican muy bien la Teoría de la Relatividad en sus libros, los cuales puedes encontrar en los Archivos de este blog. 

Finalmente, dejo enlaces a varios documentales sobre el tema:

Un saludo y feliz día de la Relatividad General!

International Physics Olympiad

La International Physics Olympiad, conocida como IPhO, es un evento anual destinado a los estudiantes pre-universitarios más destacados en la materia de Física de sus respectivos países.

Cada año, desde 1967, esta competición se ha celebrado en un país diferente. La primera fue organizada en Polonia, donde solamente participaron cinco países; y la última se ha celebrado en Bombay (India), donde han participado más de 450 alumnos de todo el mundo.

La 46th International Physics Olympiad ha tenido lugar en Bombay durante las dos primeras semanas del mes de Julio de 2015, y ha sido patrocinada por el Homi Bhabha Centre for Science Education.

En España se realizan unas pruebas locales en cada ciudad, de donde se eligen a unos representantes que se enfrentarán en la Olimpiada Española de Física. Este año se celebró en Madrid, donde tuvimos que realizar una prueba experimental y tres ejercicios teóricos.

Para ver los enunciados de la OEF, clic aquí.

De las nueve medallas de oro de la Olimpiada Española de Física, los cinco primeros fuimos a la Olimpiada Internacional de Física (celebrada en Bombay a principios de Julio de 2015) y los cuatro siguientes irán a la Olimpiada Iberoamericana de Física en el mes de Septiembre.

Algunas fotos de la IPhO:

Delegación española junto con la siria

Delegación española

Delegación española en el acto de apertura

El autor de este blog

Equipo español en el acto de clausura

Para los que estéis interesados en echar un vistazo a los enunciados del examen y sus soluciones, clic aquí.

¿Es posible la vida extraterrestre?

Enrico Fermi fue un físico italiano del siglo XX. Durante la II GM participó en el desarrollo de la bomba atómica, en el que se conoce como Proyecto Manhattan. El Fermio (elemento químico de símbolo Fm) y los fermiones (en el modelo estándar, familia de partículas constituyentes de la materia) le deben su nombre. En el año 1950 propuso la famosa Paradoja de Fermi en contraposición a la Ecuación de Drake. ¿Qué dice cada una?

Ecuación de Drake

La ecuación de Drake tiene en cuenta una serie de factores como el número de estrellas que se crean al año, la probabilidad de que desarrollen planetas en la zona habitable, de que desarrollen vida y que esta sea inteligente (entre otros parámetros) para calcular el número de civilizaciones inteligentes en nuestro universo. Resolviendo la ecuación obtuvo que debería haber 10 civilizaciones extraterrestres sólo en nuestra galaxia. Otros científicos proponen valores entre diez millones de civilizaciones y una sola: nosotros. Estas discrepancias son debidas a que no es posible tener en cuenta todos los factores de la ecuación, a que puede haber otros mecanismos de vida basados en otras estructuras moleculares (silicio, flúor, amoniaco…), o una imprecisión en esos datos que Drake obtuvo, ya que no podemos conocer con precisión el número de estrellas existentes o sus ciclos formativos. El número de civilizaciones inteligentes de nuestra galaxia se conseguiría, según Drake, multiplicando el número de estrellas que nacen cada año por la probabilidad de que tengan planetas, multiplicado por la fracción de éstos en la zona habitable, por la probabilidad de que desarrollen vida inteligente, por la fracción de que esa vida inteligente desee y pueda comunicarse y finalmente, multiplicado por el tiempo que puede existir esa civilización antes de su autodestrucción. Es demasiado simple para considerarse algo científico ya que no tiene en cuenta apenas ningún parámetro.

Si Drake tuviese razón, ¿dónde se esconden esas civilizaciones? A esta pregunta intenta responder la Paradoja de Fermi:

“La creencia común de que el Universo posee numerosas civilizaciones avanzadas tecnológicamente, combinada con nuestras observaciones que sugieren todo lo contrario es paradójica sugiriendo que nuestro conocimiento o nuestras observaciones son defectuosas o incompletas”. En la época en que la planteó, Fermi estaba trabajando en la bomba atómica, por lo que predijo lo que les sucedería a las civilizaciones avanzadas tecnológicamente: se auto aniquilarían. ¿Por qué no detectamos vida inteligente? Según Fermi, su elevada inteligencia les llevaría a su autodestrucción, prediciendo así el posible destino de la Humanidad. Otros científicos piensan que es la escasez de recursos lo que acaba con las civilizaciones inteligentes (debido a un crecimiento en forma de J o exponencial). Otros en cambio opinan que las condiciones del universo solo permiten la vida de nuestra especie (principio antrópico). Multitud de teorías científicas que pueden confundirse con especulaciones de ciencia ficción sin claros argumentos científicos.

Enrico Fermi señalando una ecuación de Einstein

Para saber si hay vida en otros planetas, primero debemos especificar qué es la vida. ¿Puede existir vida con otros elementos que no sean el carbono, hidrógeno, oxígeno…? ¿Qué tiene la Tierra de especial para haber desarrollado vida? Y multitud de preguntas más. Para generar vida, un planeta necesita de unas moléculas sencillas capaces de combinarse mediante la energía de una estrella, en nuestro caso del Sol. El planeta deberá encontrarse, según los elementos que posea, a una determinada distancia de su estrella. Si esas moléculas fuesen derivadas del amoniaco, cabe esperar que para que se desarrolle vida se encuentre a una distancia relativamente lejana de la estrella (aunque siempre dependerá del tamaño, edad y temperatura de la misma). Si por el contrario abundasen fluorocarburos, la distancia debería ser menor. Es evidente que la ecuación de Drake es demasiado simple, ya que hay más tipos de vida y no todas las estrellas son iguales. La presencia de campo magnético, de atmósfera, el tamaño y campo gravitatorio tanto del planeta como de su estrella, y así como las longitudes de onda de emisión de la estrella son factores importantes a tener en cuenta.

Nuevas investigaciones sostienen que la vida en la Tierra también es debida a la tectónica de placas, generada posiblemente por asteroides que nos visitaron en los inicios de nuestro planeta. Según el geofísico Tilman Spohn, la presencia de movimiento de las placas tectónicas hace posible la vida debido a que favorece los movimientos de materia y energía en los ciclos biogeoquímicos. Para que la corteza se dividiese en placas, geólogos y físicos como el profesor Norm Sleep (geofísico de la Universidad de Stamford) proponen la idea de que los causantes fuesen los impactos de meteoritos de hace 4.000 millones de años. En la Tierra es difícil detectarlos, debido precisamente a esa tectónica, pero en la Luna puede haber cráteres de esa edad.

Placas tectónicas en nuestro planeta

En Sudáfrica han encontrado una zona con sedimentos de hace más de 3.500 millones de años. En ellos, como ocurre en el límite KT (capa sedimentaria de iridio que dejó un asteroide que se cree como el causante hace 65 millones de años de la extinción de los dinosaurios y de los amonites), se han encontrado restos de elementos poco comunes en la corteza, como iridio, platino o cromo. Un gran avance en esta investigación sería el descubrimiento de algunos de esos cráteres. Cabe esperar que estas capas tan antiguas sean la muestra de que la Tierra estuvo bañada de asteroides en sus orígenes, lo que ayudó notablemente al desarrollo de la tectónica de placas, que combinada con la energía gravitacional y la energía interna del interior, permiten hoy día ese continuo desplazamiento horizontal de las placas litosféricas. Aún no sabemos si una tectónica de placas es indispensable para la vida. Si así lo fuese, otro factor más a tener en cuenta en la ecuación de Drake.

Capa oscura rica en Iridio que marca
el límite K-T

En mi opinión, es muy probable la existencia de vida extraterrestre. Más difícil es la existencia de vida inteligente, pero también posible. Organizaciones como el SETI están completamente convencidas de encontrar señales de vida inteligente antes de fin de siglo. El universo es muy grande y tiene mucha edad. Quizá en algún lugar lejano se hayan preguntado lo mismo, o incluso lo estén haciendo en este momento, aunque nuestro “rango de visión” (debido a la relativa lentitud de la velocidad de la luz) sea muy pequeño y nunca los encontremos. Quizá Drake sí que tuviese razón, ya que la probabilidad de encontrar un planeta con exactamente las mismas características que la Tierra es cada vez mayor, y si así fuese sería muy posible el desarrollo de la vida, y posiblemente también alguna especie que pueda llegar a auto considerarse como “inteligente”, teniendo en cuenta que lo que conocemos como vida es solo una de tantas posibilidades.

Espero que os haya gustado hoy esta entrada un poco diferente a las que suelo publicar.

Un saludo!

Cinemática y Gravitación

¿De qué depende el tiempo que tarda en caer un objeto en caída libre?

Como es lógico, de la altura. ¿Pero y la aceleración? ¿Es constante siempre? La respuesta es que no.

Esa aceleración se debe una fuerza de carácter gravitatorio, que a su vez depende de la distancia entre los cuerpos y sus masas (Ley de la Gravitación Universal). Como la fuerza aumenta conforme al objeto se acerque a la Tierra, también lo hará la aceleración para una masa m constante. Por esto, he decidido combinar las ecuaciones de cinemática con las de gravitación, para obtener unas nuevas que relacionen el tiempo de caída con la altura (teniendo en cuenta una aceleración variable). 

Esto quiere decir que la aceleración que sufre nuestro objeto depende de la altura, y nuestro objetivo será hallar la aceleración media entre el momento en el que está arriba del todo y el momento en el que toca el suelo. Recordemos las constantes con las que vamos a trabajar:

Si graficamos la aceleración en función de la altura, obtenemos una gráfica del siguiente tipo: (función potencial de exponente entero negativo par)

Cuando la altura vale 0, se obtiene el conocido valor de 9,8 m/s2 para la aceleración. A medida que la altura aumenta, este valor tiende a 0 en el infinito. Podemos observar que debajo de la función se forma un área:

Este área (A) corresponde geométricamente con la integral definida en el intervalo [0, h] de la función aceleración. Recordemos que la aceleración es la derivada de la velocidad con respecto al tiempo, entonces la integral indefinida de la función aceleración (diferencial de tiempo) corresponde con la función velocidad, que depende del tiempo con una aceleración constante. Podemos decir entonces que el área A se corresponde con la aceleración multiplicada por el tiempo. Podemos hallar la aceleración media así:

Esta nueva función tiene aceleración constante, y el área (A) de debajo en el intervalo [0, h] es la misma. Por eso podemos decir que la aceleración media se corresponde con ese área dividida entre h. Viéndolo como si fuese un rectángulo, el área A sería igual a la base h por la altura am.

Vamos a comparar las ecuaciones obtenidas con las ecuaciones "normales" donde consideramos la aceleración, g, constante:

Graficando las dos ecuaciones del tiempo con respecto a la altura obtenemos lo siguiente:

La altura (h) está representada en el eje de abscisas en km, y el tiempo (t) está representado en el eje de ordenadas en segundos. La línea negra es la fórmula con aceleración constante, y la línea roja es la que hemos hallado, donde la aceleración es variable.

Podemos observar que a alturas "pequeñas" las dos funciones están casi superpuestas. A partir de 300 o 400 km ya se observan diferencias que se van acrecentando con el tiempo. Para que nos hagamos una idea, la altura desde donde se lanzó Felix Baumgartner está representada por la línea azul, es decir, la diferencia de tiempos no alcanzaba ni 1 segundo.

Si representamos la altura de un objeto en función del tiempo que tarda en caer según las dos fórmulas:

De nuevo, la línea roja será la que hemos hallado en esta entrada y la negra la que considera la aceleración constante. A alturas bajas, hasta los 300 km, la diferencia es insignificante. A partir de esa altura, es un factor a tener en cuenta. Una altura de 200 km representa tan solo el 3% del radio terrestre.

Finalizaré la entrada recordando las dos ecuaciones que hemos hallado hoy, la que relaciona la altura (h) con respecto al tiempo y la que relaciona el tiempo (t) con respecto a la altura desde la que se lanza un cuerpo en caída libre:

Nota: considero todos los tiempos, lógicamente, como positivos si no pongo el símbolo "+" delante de las raíces.

Estas ecuaciones se pueden aplicar en otros planetas, sustituyeno el radio y la masa por el que corresponda. Es necesario decir también que en estas ecuaciones omitimos por completo el rozamiento con el aire, que es un factor muy a tener en cuenta. Los tiempos que hallemos con estas fórmulas serán ligeramente superiores a los experimentales por este motivo. Posteriormente ampliaré las ecuaciones teniendo en cuenta esos datos.

Hasta dentro de unos días con otra entrada. Espero que os haya gustado esta, ya que le he dedicado bastante tiempo entre obtener las ecuaciones y preparar la entrada y las gráficas.

Un saludo!

Paradoja de los Gemelos

Y finalmente llegamos al final de esta serie dedicada especialmente a Relatividad Especial. Si quieres leer el resto de entradas sobre este tema, te invito a que hagas clic en el siguiente enlace, donde están todas agrupadas: Serie de Relatividad Especial.

Hoy vamos a tratar la Paradoja de los Gemelos. Antes de todo, veamos en qué consiste:

"Dos hermanos gemelos deciden hacer un peculiar experimento: uno de ellos es astronauta, y se embarca en un viaje espacial a velocidades próximas a la de la luz. Para el que permaneció en la Tierra, el astronauta ha sido el que se ha movido, por tanto al regresar habrá envejecido menos que él (de acuerdo con la dilatación temporal que sufre a esas velocidades). Pero para el astronauta, el que se ha movido respecto a él ha sido el resto del Universo...por tanto al volver, el que menos habrá envejecido habrá sido el que permaneció aquí".

Aquí reside la paradoja, ya que lo que miden los dos no tiene sentido en el momento en el que se encuentran. Si analizamos a fondo el experimento, veremos qué gemelo tiene razón. ¿Te apuntas?

Antes de nada, recordemos que a grandes velocidades el tiempo se ralentiza, el espacio se contrae y la masa aumenta. Vamos a observar el experimento desde el punto de referencia del gemelo astronauta primero, y finalmente el otro gemelo. De este modo queremos saber qué ocurre exactamente y cuál de los dos envejece más. Vamos a añadir un matiz: tanto el astronauta como su hermano tienen una linterna con la que envían un destello cada segundo a su hermano.

El astronauta decide embarcarse en su travesía espacial de 10 años luz a 261.000 km/s (he escogido este valor para simplificar las cuentas al final). El astronauta no mide 10 años luz, sino que debido a la contracción espacial que experimenta, para él el trayecto es de 5 años luz. A la velocidad que lleva, debería tardar 11,5 años ida y vuelta en completar el trayecto. Sin embargo, para el que permanece en la Tierra no es así...

Aunque el hermano que se queda en la Tierra encienda y apague su linterna cada segundo, el astronauta no ve esos destellos cada segundo, porque cada segundo la luz tiene que recorrer una distancia de 261.000 km más (el espacio que recorre su nave en un segundo). Debido a esto, los destellos se ralentizan cada 1,87 segundos...y si aplicamos la fórmula de dilatación temporal...los destellos se producirán cada 3,74 segundos.

Hemos dicho que para el astronauta, el tiempo de ida y vuelta son 11,5 años, entonces en ir emplearía la mitad, un total de 5,75 años. Como el tiempo en la Tierra transcurre 3,74 veces más lento, el tiempo que habrá medido el hermano de la Tierra será 5,75/3,74...es decir, 1,5 años.

Cuando el astronauta llega a su destino y se da la vuelta, el proceso se invierte. Cada segundo, la luz tiene que recorrer 261.000 km menos, lo que provoca que esos destellos los perciba cada 0,26 segundos teniendo en cuenta la dilatación temporal. Entonces, los 5,75 años de vuelta de la nave para nosotros son como 21,5 años, el resultado de dividir 5,75/0,26.

Astronauta: 5,75 + 5,75 = 11,5 años

Tierra: 1,5 + 21,5 = 23 años

Si hacemos cuentas, el astronauta ha vivido 11,5 años en total y nosotros en la Tierra hemos vivido 23 años, el doble, exactamente el mismo resultado que obtendríamos según la transformación de Lorentz.

Según la primera parte de este experimento, el que menos envejece es el astronauta.

Ahora vamos a centrarnos en el hermano que permanece en nuestro planeta. Al igual que antes, los destellos de su hermano le llegan cada 3,74 segundos. La distancia que recorre su gemelo son 10 años luz a un 87% de la velocidad de la luz, entonces la nave tarda 11,5 años "terrestres" en llegar al destino.

Cuando el astronauta llega al final de la travesía y se da la vuelta, en la Tierra vamos a seguir notando los destellos cada 3,74 segundos durante 10 años más, porque se encuentra a 10 años luz de nosotros. Eso quiere decir que pasamos un total de 21,5 años percibiendo los destellos, lo que para el astronauta serían 5,7 años.

Como el viaje de vuelta dura 11,5 años (10 años luz a 261.000 km/s), y 10 de esos años los percibimos cada 3,74 segundos, quedan 1,5 años. A partir de ese momento, desde la Tierra comenzamos a percibir los destellos aceleradamente, porque ya ha llegado el último que se emitió desde el punto más lejano a 10 años luz. Durante esos 1,5 años, los destellos se producen cada 0,26 segundos. Eso quiere decir que para el tripulante de la nave, ese año y medio equivale a 1,5/0,26 = 5,7 años.

Astronauta: 5,7 + 5,7 = 11,5 años

Tierra: 11,5 + 10 + 1,5 = 23 años

Si echamos cuentas, el astronauta ha vivido 11,5 años y en la Tierra han pasado 23 años. Exactamente el mismo resultado que en el caso anterior. Aquí queda resuelta la paradoja.

El gemelo que envejece menos es el astronauta.

En ambos casos se cumple que el que menos envejece es el astronauta, tal y como predicen las ecuaciones de Lorentz y Einstein.

No hemos tenido en cuenta la dilatación temporal producida por la gravedad, que también afectaría al experimento. El gemelo de la Tierra se encuentra en un sistema acelerado constante (la aceleración de la gravedad sería g = 8,81 m/s2), pero el astronauta también tendría que acelerar para lograr tales velocidades, por lo que los datos del experimento podrían variar teniendo en cuenta estas consideraciones.

Aquí llegamos al final de la serie dedicada a Relatividad Especial. Espero que os haya gustado, y como ya sabéis, aquí abajo podéis dejar comentarios.

¡Un abrazo científico!

Péndulo de Foucault

Hoy en día, gracias a la existencia de satélites, podemos comprobar que la Tierra se mueve. Pero, ¿cómo demostró esto León Foucault hace más de 150 años?

Primero debemos recordar la Ley de la Inercia de Newton, publicada en su famoso libro Principia Mathematica, que es además el libro donde nace la física moderna. Esta ley dice que todo cuerpo conservará su estado de reposo o de movimiento rectilineo uniforme a no ser que actúe una fuerza (o varias cuya resultante no sea nula) sobre él. Esto indica que un cuerpo sobre el que no actue una fuerza no va a variar su movimiento. Una pelota que se mueva en línea recta no variará su movimiento si no hay fuerzas que actúen sobre ella.

En un péndulo "ideal", la energía mecánica se conserva. La energía cinética (relacionada con la velocidad) más la potencial (relacionada con la altura) en cualquier punto siempre será la misma y, si no tenemos en cuenta el rozamiento, sobre él no actuará más fuerzas que la gravedad. Entonces el péndulo siempre se moverá en línea recta si no aplicamos fuerzas sobre él. 

El experimento que realizó Foucault a mediados del siglo XIX fue colgar una bola de cañón de la cúpula de una catedral a modo de péndulo. En la parte de abajo colocó una aguja para que el péndulo dejase marcada su trayectoria en el suelo, tal que así:

Bola de cañón con aguja abajo para dejar la marca de su trayectoria

Después de varias horas de oscilación del péndulo, el resultado del experimento fue el siguiente:

Resultado del experimento de Foucault

Bajo el péndulo se apreciaban marcas como las del dibujo. Si el movimiento del péndulo es rectilineo, pero aparentemente "va girando", quiere decir que "el suelo se mueve bajo el péndulo". Dicho de otro modo, la Tierra se mueve. 

Debido a la rotación terrestre, y dado que el péndulo no cambia de dirección nunca, observamos que la trayectoria del péndulo parece ir rotando, cuando lo único que rota es nuestro planeta. La explicación técnica a este efecto la encontramos en el efecto Coriolis, una fuerza originada debido a la rotación terrestre que es la causante del giro de los huracanes. Puedes leerla aquí.

Puedes realizar un símil de este experimento en casa, colocando una cartulina en el suelo y colgando del techo una cuerda atada a algo esférico (no demasiado ligero) y a una mina de lápiz. Mientras dure el efecto de la oscilación, ve moviendo la cartulina como si fuese nuestro planeta rotando sobre sí mismo. También puedes esperar a que ocurra de forma natural, pero necesitas paciencia...

Evidentemente este aparente movimiento no será igual en todos los puntos del planeta. Mientras que en los polos el péndulo tarda 24 horas en completar una vuelta (lo que tarda la Tierra en dar una vuelta sobre sí misma), a medida que nos acerquemos al ecuador tardará más. En el ecuador, dado que el plano de oscilación es perpendicular al eje de rotación, el péndulo oscilará en la misma linea siempre. La fórmula que relaciona el periodo (tiempo en volver a un mismo plano de oscilación) y la latitud a la que se encuentre el péndulo, es la siguiente: 

T=24/sen ß  siendo ß el ángulo de la latitud donde se encuentre el péndulo.

A partir de la fórmula deducimos que en los polos (latitud 90º, sen 90º = 1) el periodo es de un día, mientras que en el ecuador no existe periodo dado que no varía el plano de oscilación. En Salamanca, una ciudad de España con una latitud de 40º 58', el tiempo que tarda el péndulo en completar una vuelta es de 36 horas y 36 minutos. 

Las siguiente fotografías y el vídeo pertenecen al péndulo de la Facultad de Físicas de la Universidad de esta ciudad, Salamanca:

Al igual que en la mayoría de facultades de Ciencias, este péndulo lo hallamos en miles de museos por todo el mundo, dada su gran relevancia. 

Gracias por haber leído esta entrada. Compartidla a quién penséis que le pueda interesar.

Nos vemos en la próxima.

¡UN SALUDO!