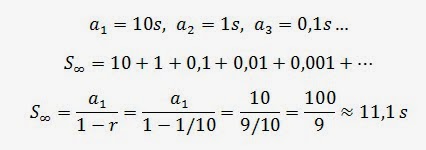El efecto Hall

Edwin Herbert Hall (1855-1938) fue un físico estadounidense que trabajó en Harvard, donde como estudiante de doctorado descubrió el efecto que lleva su nombre.

A grandes rasgos, el Efecto Hall consiste en la aparición de una diferencia de potencial eléctrico entre los extremos de un conductor atravesado por un campo magnético por el que circula una corriente.

Esquema ilustrativo del Efecto Hall

Imaginemos que nos encontramos en la década de 1870, cuando el Electromagnetismo es aún un gran desconocido. Todavía quedan muchos años para el descubrimiento del electrón (Thomson, 1897) y para la formulación de la Fuerza de Lorentz.

Las corrientes eléctricas eran un misterio, pero gracias al Efecto Hall se pudo saber que los portadores de carga que se desplazaban por los cables conductores eran negativos. Intentemos entenderlo desde el principio:

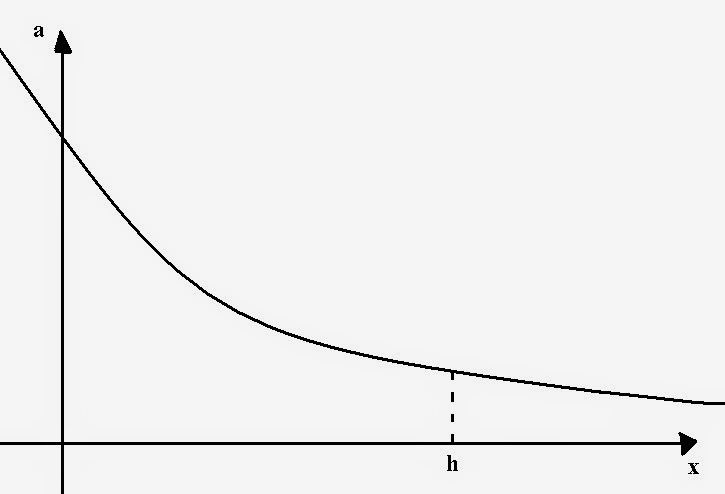
Sea un conductor plano de dimensiones transversales a y b recorrido por una intensidad I y atravesado por un campo magnético B, como se esquematiza en la ilustración inferior.

fig. 2

La fuerza de Lorentz aparece sobre cargas en movimiento en el interior de campos magnéticos, y el módulo de dicha fuerza es el producto del módulo del campo multiplicado por la velocidad y la carga (F = qvB). Su dirección es perpendicular a B y a v, y su sentido depende también de si la carga es positiva o negativa.

Es obvio que sobre las cargas que circulan por el conductor aparecerá una fuerza de Lorentz de sentido ascendente, de forma que los electrones (los portadores) se acumularán en la zona superior de la fig. 2, y que la zona inferior se cargará positivamente.

Como consecuencia de esa reordenación de las cargas, se formará un campo eléctrico uniforme que parte de la zona cargada positivamente hacia la zona cargada negativamente, de forma que tiende a anular la fuerza de Lorentz. Cuando el módulo de ambas fuerzas (magnética y eléctrica) sean iguales, aparecerá un voltaje constante en el tiempo llamado Voltaje Hall. De forma cuantitativa:

Una importante consecuencia de este efecto viene dada por el estudio del signo del voltaje observado. Veamos cómo se determinó que la carga de los portadores de corriente eléctrica (aún no se había descubierto el electrón) era negativa:

Como experimentalmente se determinó que el voltaje en B era menor que en A, el campo eléctrico estaba dirigido hacia arriba, y por consiguiente la fuerza de Lorentz tendría que dirigirse hacia abajo. De esta manera se supo que los portadores de corriente eléctrica poseían carga negativa.

Además de poder medir la carga del electrón, podemos usar el efecto Hall para medir la intensidad y el sentido de campos magnéticos, de corrientes eléctricas e incluso la densidad electrónica de materiales conductores y semiconductores. Se usa también en automovilismo, en música, en lectores de CD y en muchos más campos.

Sensor de proximidad basado en el Efecto Hall

Deducción de la 1ª Ley de Kepler

En entradas anteriores hemos hablado de las Tres Leyes de Kepler, como puedes leer en Deducción de la Tercera Ley de Kepler y Deducción de la Segunda Ley de Kepler.

En la entrada de hoy vamos a deducir la Primera Ley de Kepler, que dice así: "Los planetas describen órbitas elípticas planas en torno al Sol, situado en uno de sus focos". Para ello tendremos que saber por qué son órbitas planas y por qué son elípticas.

Para demostrar que son planas vamos a partir de un concepto ya mencionado en la Deducción de la Segunda Ley de Kepler: el momento angular es constante en toda la órbita.

Al ser L (vector) constante, también lo serán r (vector) y el momento lineal (vector), r y p estarán siempre en el mismo plano, y por eso las órbitas son planas. Queda demostrar que la curva que describen los planetas es una elipse:

Imaginemos que se trata de una órbita desconocida, y que nuestro objetivo es hallar la ecuación de la misma:

A partir de esas definiciones vamos a intentar sacar la ecuación buscada.

Partiendo también de la definición de energía mecánica y despejando la velocidad normal:

Hacemos el siguiente cambio de variable:

Con lo que llegamos a la ecuación de una elipse en forma polar, cuya excentricidad depende de C y B, y estos a su vez de G, M, m, L y Em.

Una vez demostrada la Primera Ley de Kepler, hemos acabado con este conjunto de entradas sobre las Leyes de Kepler.

Un saludo! Hasta la próxima y FELIZ NAVIDAD!

Deducción de la Segunda Ley de Kepler

Hará cosa de medio año, en este blog deducimos la Tercera Ley de Kepler, o mejor dicho, la justificamos a partir de la Ley de la Gravitación Universal.

Hoy justificaremos la 2ª Ley de Kepler, que dice así: "Las áreas barridas por un radio vector con origen el Sol y destino un planeta, barren áreas iguales en tiempos iguales". Se verá mejor con una imagen:

Si el tiempo que tarda un planeta en ir desde P1 hasta P2 es el mismo que en ir desde P3 hasta P4, el área A1 será igual al área A2. Pero, ¿por qué ocurre esto?

Johannes Kepler se basó en los datos astronómicos de su coetáneo Tycho Brahe antes de que Isaac Newton estableciese su Ley de la Gravitación Universal. Nosotros vamos a partir de ahí, pero primero definamos algunos términos:

Perigeo: punto de la órbita más cercano al Sol (o al astro en torno al cual se orbite). En el caso de la Tierra, se llama Perihelio.

Apogeo: punto de la órbita mas alejado del Sol. En el caso de la Tierra se llama Afelio.

Velocidad Areolar: el área barrida por el radio vector por unidad de tiempo.

Demostración:

Primero vamos a demostrar esta ley en los casos particulares del apogeo y perigeo. Si consideramos un diferencial de tiempo (dt), el área barrida por el planeta se asemeja a un triángulo de base ds y de altura la distancia al Sol:

Calculemos el área de las zonas rojas (dA) como si fuesen triángulos:

En el caso del perigeo procederemos del mismo modo:

Ahora vamos a calcular el momento de fuerza de la fuerza gravitatoria del Sol al planeta con respecto al propio Sol. Por definición:

Entonces el momento será (modularmente):

El momento también puede escribirse de la siguiente forma:

Deducimos que el momento angular es constante (en dirección, sentido y módulo) a lo largo de toda la trayectoria. El momento angular se define como:

Como hemos dicho que el momento angular es constante, el momento angular en el apogeo será igual al del perigeo:

Finalmente llegamos a que la velocidad areolar en el perigeo es igual a la velocidad areolar en el apogeo:

Para cualquier otro punto de la órbita procedemos igual:

El área (dA):

Y como tanto L como m son constantes, la velocidad areolar también será constante y queda demostrada la Segunda Ley de Kepler.

Puedes leer también la demostración de la Primera Ley de Kepler.

Nos vemos en la próxima entrada!

Resolviendo la paradoja de Aquiles y la tortuga

Zenón de Elea fue un filósofo griego muy conocido por plantear numerosas paradojas relacionadas con el movimiento. De entre todas ellas, la más famosa puede que sea la de Aquiles y la tortuga. 

Aquiles decide echar una carrera a una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.

Todos sabemos que Aquiles ganará de sobra la carrera, igual que pensaba Zenón. Zenón planteó 40 paradojas de este estilo, debatiendo sobre el espacio, el tiempo y el movimiento. Proponía estos ejercicios mentales para reducir al absurdo las teorías de que la suma de infinitos números tenga que dar infinito. 

Si la suma de infinitos sumandos siempre fuese igual a infinito, Aquiles nunca ganará la carrera, pero esto matemáticamente y físicamente no es así. 

Supongamos que la velocidad de la tortuga es de 1 m/s, la velocidad de Aquiles es de 10 m/s y la ventaja inicial es de 100 m. En solo 10 segundos, Aquiles habrá alcanzado el punto desde el que sale la tortuga, y esta habrá avanzado 10 metros más. Esos 10 metros los recorre Aquiles en 1 segundo, pero la tortuga habrá avanzado 0,1 metros más...y así sucesivamente. Lo que plantea la paradoja es que 10 + 1 + 0,1 + ... da como resultado infinito, pero eso es incorrecto.

Cada vez, Aquiles tarda 10 veces menos en recorrer el trozo que lo separa de la tortuga. Esta fórmula nos puede ayudar a conocer todos los tiempos empleados (progresión geométrica decreciente):

Sucesión de tiempos empleados
expresada en segundos

Aplicando una fórmula que no vamos a demostrar ahora (fórmula de la suma de los infinitos términos de una progresión geométrica decreciente), podemos hallar la suma de esos tiempos. La demostración se realizaría restando a la suma de todos los términos, la suma multiplicada por la razón, pero por comodidad no lo vamos a hacer.

Como vemos en la imagen superior, la suma de 10 + 1 + 0,1...da como resultado 11,1 segundos. Aunque haya infinitos sumandos, el resultado es finito. Esto demuestra que Aquiles alcanza a la tortuga y lógicamente gana la carrera.

Podemos resolverlo también utilizando las leyes del movimiento, ya que conocemos las velocidades de ambos corredores la diferencia de posiciones. Igualando las posiciones conseguimos despejar el tiempo transcurrido en cruzarse.

Por lo tanto, una suma de infinitos términos decrecientes puede dar un resultado finito, como en este caso.

Un saludo, nos vemos en la próxima. No os olvidéis de compartir esta entrada!

Cinemática y Gravitación

¿De qué depende el tiempo que tarda en caer un objeto en caída libre?

Como es lógico, de la altura. ¿Pero y la aceleración? ¿Es constante siempre? La respuesta es que no.

Esa aceleración se debe una fuerza de carácter gravitatorio, que a su vez depende de la distancia entre los cuerpos y sus masas (Ley de la Gravitación Universal). Como la fuerza aumenta conforme al objeto se acerque a la Tierra, también lo hará la aceleración para una masa m constante. Por esto, he decidido combinar las ecuaciones de cinemática con las de gravitación, para obtener unas nuevas que relacionen el tiempo de caída con la altura (teniendo en cuenta una aceleración variable). 

Esto quiere decir que la aceleración que sufre nuestro objeto depende de la altura, y nuestro objetivo será hallar la aceleración media entre el momento en el que está arriba del todo y el momento en el que toca el suelo. Recordemos las constantes con las que vamos a trabajar:

Si graficamos la aceleración en función de la altura, obtenemos una gráfica del siguiente tipo: (función potencial de exponente entero negativo par)

Cuando la altura vale 0, se obtiene el conocido valor de 9,8 m/s2 para la aceleración. A medida que la altura aumenta, este valor tiende a 0 en el infinito. Podemos observar que debajo de la función se forma un área:

Este área (A) corresponde geométricamente con la integral definida en el intervalo [0, h] de la función aceleración. Recordemos que la aceleración es la derivada de la velocidad con respecto al tiempo, entonces la integral indefinida de la función aceleración (diferencial de tiempo) corresponde con la función velocidad, que depende del tiempo con una aceleración constante. Podemos decir entonces que el área A se corresponde con la aceleración multiplicada por el tiempo. Podemos hallar la aceleración media así:

Esta nueva función tiene aceleración constante, y el área (A) de debajo en el intervalo [0, h] es la misma. Por eso podemos decir que la aceleración media se corresponde con ese área dividida entre h. Viéndolo como si fuese un rectángulo, el área A sería igual a la base h por la altura am.

Vamos a comparar las ecuaciones obtenidas con las ecuaciones "normales" donde consideramos la aceleración, g, constante:

Graficando las dos ecuaciones del tiempo con respecto a la altura obtenemos lo siguiente:

La altura (h) está representada en el eje de abscisas en km, y el tiempo (t) está representado en el eje de ordenadas en segundos. La línea negra es la fórmula con aceleración constante, y la línea roja es la que hemos hallado, donde la aceleración es variable.

Podemos observar que a alturas "pequeñas" las dos funciones están casi superpuestas. A partir de 300 o 400 km ya se observan diferencias que se van acrecentando con el tiempo. Para que nos hagamos una idea, la altura desde donde se lanzó Felix Baumgartner está representada por la línea azul, es decir, la diferencia de tiempos no alcanzaba ni 1 segundo.

Si representamos la altura de un objeto en función del tiempo que tarda en caer según las dos fórmulas:

De nuevo, la línea roja será la que hemos hallado en esta entrada y la negra la que considera la aceleración constante. A alturas bajas, hasta los 300 km, la diferencia es insignificante. A partir de esa altura, es un factor a tener en cuenta. Una altura de 200 km representa tan solo el 3% del radio terrestre.

Finalizaré la entrada recordando las dos ecuaciones que hemos hallado hoy, la que relaciona la altura (h) con respecto al tiempo y la que relaciona el tiempo (t) con respecto a la altura desde la que se lanza un cuerpo en caída libre:

Nota: considero todos los tiempos, lógicamente, como positivos si no pongo el símbolo "+" delante de las raíces.

Estas ecuaciones se pueden aplicar en otros planetas, sustituyeno el radio y la masa por el que corresponda. Es necesario decir también que en estas ecuaciones omitimos por completo el rozamiento con el aire, que es un factor muy a tener en cuenta. Los tiempos que hallemos con estas fórmulas serán ligeramente superiores a los experimentales por este motivo. Posteriormente ampliaré las ecuaciones teniendo en cuenta esos datos.

Hasta dentro de unos días con otra entrada. Espero que os haya gustado esta, ya que le he dedicado bastante tiempo entre obtener las ecuaciones y preparar la entrada y las gráficas.

Un saludo!