La materia oscura

La materia oscura es uno de los conceptos que más veces le rondan por la cabeza a los físicos desde mediados del siglo pasado. Veamos qué es este concepto.

Debido a una epidemia de peste, un joven llamado Isaac Newton abandonó temporalmente sus estudios en Cambridge y se retiró a Woolsthorpe, donde entre 1665 y 1667 dedujo las leyes de la mecánica newtoniana, el cálculo diferencial y la Ley de la Gravitación Universal:

$\vec{F}=-G\displaystyle\frac{Mm}{r^3}\vec{r}$

De este modo fue capaz de aunar en una sola ecuación cielo y tierra, ya que la fuerza que hacía caer una manzana de un árbol era la misma que la que mantenía a la Luna en órbita circular.

Ya en tiempos de Galileo se conocía que la aceleración de la gravedad era aproximadamente $g_0=9,8 m/s^2$. Por la segunda ley de Newton, tendríamos que $g_0R_T^2=GM_T$. Como el radio de la Tierra era ya conocido, Newton sabía ya el valor de $G\cdot M$. Igualando la aceleración de la gravedad terrestre sobre la Luna a la fuerza centrípeta, y conocido el radio orbital lunar, Newton predijo con total exactitud el periodo de traslación de la Luna alrededor de nuestro planeta. De este maravilloso modo, especialmente una vez determinado el valor de $G$ por Cavendish en 1798, se podrá determinar la masa de cualquier cuerpo midiendo la velocidad de un cuerpo que orbite en torno a él por la formulita:

$v=\sqrt{\displaystyle\frac{GM}{r}}$

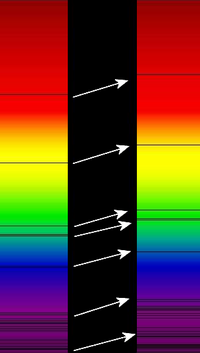
En los años setenta del siglo pasado, se intentó hacer lo mismo con las galaxias, es decir, determinar sus masas a partir de las velocidades de las estrellas que las componen. Como es muy complicado medir la velocidad de las estrellas alrededor de las galaxias, se utiliza el efecto Doppler y el corrimiento al rojo de los espectros emitidos por las estrellas para deteminar sus velocidades.

A esto se dedicaron los científicos Vera Rubin y Kent Ford, midiendo datos de más de sesenta galaxias cuando se dieron cuenta de algo. En efecto, es previsible que cuando más lejos se encuentre una estrella del centro de la galaxia, más despacio debería moverse. Pero lo que realmente ocurría era que todas las estrellas parecían moverse a la misma velocidad. En el gráfico superior, se esperaba que ocurriese algo como (A) pero lo que realmente ocurría era (B). Las soluciones eran simples: o la Ley de Newton no era válida en esos casos...o existía una extraña materia que aumentaba enormemente la masa total de la galaxia: la materia oscura.

Sin meternos en muchos berenjenales, algunos físicos defendían teorías tipo MOND, acrónimo en inglés de Modified Newtonian Dynamics. Defendían incluso que $G$ no era una constante, sino que $G=G(r)$, es decir, que $G$ aumentaba cuando las distancias entre los astros eran grandes, y de ese modo no era necesario postular la existencia de materia oscura. 

En 1915, Einstein presentó su Teoría de la Relatividad General, con lo que pudo comprobar aquellos "huecos" en los que la teoría de Newton no era muy precisa. Un claro ejemplo es la precesión del perihelio de Mercurio. Con ésta, podemos hacer la siguiente corrección a la Ley de la Gravitación Universal:

$F=G\displaystyle\frac{Mm}{r^2}-\displaystyle\frac{4}{c^2}\cdot \displaystyle\frac{G^2M^2m}{r^3}+...$

Pero aún así no conseguimos solucionar el problema que nos atañe. La solución está en otro fenómeno derivado del genio de Einstein: las lentes gravitacionales.

La masa, según la Teoría de la Relatividad, curva el espacio-tiempo. Esa curvatura es capaz de desviar rayos luminosos. El efecto de una lente gravitacional es la curvatura de los rayos de luz que provienen desde detrás de la lente. El ángulo de desviación es proporcional a la masa de la "lente gravitacional", de modo que disponemos de un método alternativo para conocer las masas de galaxias o cúmulos galácticos. Lo sorprendente es que esta masa resulta ser la misma que la calculada por la Ley de Newton, es decir, tiene que existir esa materia oscura para "rellenar esa masa que nos falta".

Cúmulo "bala" estudiado como choque entre galaxias

En realidad, la mayoría de científicos rechazan las teorías MOND gracias al estudio de choques entre galaxias. En estos choques, las nubes de gas (helio e hidrógeno principalmente) se retrasan respecto de la galaxia, pero esta sigue comportándose como una lente gravitacional, a pesar de que la mayor parte de la masa ordinaria de una galaxia se debe a la nube de gas. Esto es prueba clara de la existencia de materia oscura, de una naturaleza distinta a la de la materia ordinaria.

Gracias a un estudio exhaustivo sobre la radiación de fondo de microondas, es posible deducir la existencia de materia oscura y su proporción respecto a la materia ordinaria. A partir del mapa de la imagen inferior y del análisis de las diferencias en la densidad o temperatura de las ondas recibidas, hemos podido deducir que la densidad de materia en el Universo es un 32% de la densidad crítica, de la cual un 5% es materia ordinaria y un 27% materia oscura. Actualmente se cree que el universo es plano, es decir, que su densidad es igual a la densidad crítica, de modo que el 68% que falta corresponde a "algo" diferente: a energía oscura. Es notable mencionar que los datos teóricos obtenidos del análisis del fondo de micrrondas concuerdan a la perfección con las medidas sobre la cantidad de materia en el universo.

Fondo cósmico de micrrondas. Satélite Planck.

La pregunta ahora es: ¿de qué está hecha la materia oscura? O mejor dicho, ¿de qué no está hecha?

Debe estar formada por alguna partícula que aún no hayamos detectado, y debería interaccionar muy poco o nulamente con el resto de la materia. No puede estar formada por protones, neutrones ni electrones: de lo contrario los cálculos de la nucleosíntesis primitiva no coincidirían con los observados. Tampoco puede estar formada por partículas con carga, y debe ser muy estable, al menos su vida debería ser superior a la edad del universo. Por último, tampoco puede interaccionar mucho consigo misma y ha de ser fría, para que de este modo se agrupe de la manera en que lo hace.

Estudios realizados con supercomputadoras ofrecen mapas de materia oscura muy semejantes a los medidos experimentalmente si aceptamos como hipótesis las características antes citadas sobre la materia oscura.

Un candidato a materia oscura fue el neutrino. Debido a su baja interacción con la materia, resulta un buen partido para ser lo que llamamos "materia oscura", pero no cumple la condición de ser frío, pues tiene unas velocidades muy próximas a la de la luz. Además, deberían tener más masa para constituir el 27% de la materia del universo.

Mapa de materia oscura en el universo

La mayor parte de la comunidad científica considera el modelo estándar de la física de partículas como inacabado: es necesaria una nueva Física que explique muchas de las cosas que el modelo estándar deja a medias, entre ellas las partículas básicas constituyentes de la materia oscura. Hablaríamos entonces de partículas exóticas (WIMPs) como el neutralino (partícula super-simétrica del neutrino), los axiones...Entraríamos ya en teorías más nuevas como la Supersimetría, la Teoría de Supercuerdas y demás.

Actualmente hay decenas de experimentos que se están llevando a cabo en todo el mundo que tratan de descubrir alguna de las partículas candidatas a materia oscura, como por ejemplo el experimento ANAIS en el Pirineo aragonés. Pese a todos los esfuerzos empleados, aún no existen evidencias claras del descubrimiento de esta exótica y misteriosa materia.

El efecto marea

Como ya mencionamos hace cierto tiempo en la entrada sobre la relación entre los corales y la duración del día terrestre, el período de rotación terrestre está aumentando, es decir, la Tierra se está frenando. Debido a ello, la Luna se aleja de la Tierra. ¿Pero por qué sucede todo esto? La respuesta la encontramos en el llamado "Efecto Marea", que trataremos de analizar en la entrada de hoy.

Partimos de que el momento angular del sistema Tierra-Luna se conserva. Trataremos a la Luna como una masa puntual y despreciaremos el momento de inercia de la Tierra respecto de su eje sobre el de la Luna alrededor de la Tierra. Consideraremos, por simplicidad, que el centro de masas del sistema coincide con el centro de la Tierra.

Las llamadas fuerzas de marea generan un torque que tiende a igualar la velocidad angular de rotación terrestre con la translación de la Luna en torno a nuestro planeta, de modo que en ese momento nuestro satélite se encontrará, aparentemente, en la misma posición en el firmamento.

La conservación del momento angular nos permite escribir que

Calculando el momento de inercia lunar y terrestre, encontramos que el de la Luna es tres órdenes de magnitud superior al de la Tierra, por lo que podemos decir que

En el momento en que los períodos se igualen, se cumplirá la ecuación

que aparece tras igualar la aceleración gravitatoria a la centrípeta.

Teniendo en cuenta el momento angular del sistema, es fácil ver que

lo que implica que la distancia final entre la Tierra y la Luna es 1,4 veces la actual.

Asimismo, la velocidad angular final del sistema vendrá dada por

que se corresponde con un período de unos 46 días actuales.

¿Cuánto se separa la Luna de la Tierra cada año?

Para ello tendremos que hacer un esquema ilustrativo de las fuerzas de marea que actúan sobre la Tierra. En la entrada de hoy despreciaremos la interacción con el Sol. Podríamos considerar el sistema Tierra-Luna de la forma:

Ahora calcularemos las fuerzas que ejerce la Luna sobre cada una de los dos masas. Llamaremos F1 a la fuerza sobre la masa más próxima y F2 a la más lejana. Utilizando la Ley de la Gravitación de Newton y el Teorema del coseno, llegamos a que:

Y por consiguiente, el torque generado por el par de fuerzas sobre la Luna será:

Pero como esto es un blog de Física y a los físicos no les gustan fórmulas tan grandes y feas, vamos a embellecerla un poco. Para ello tenemos en cuenta que D >> r, y tras una serie de cálculos y aproximaciones, llegamos a:

Que es infinítamente más sencilla, totalmente válida y más bonita. Para obtenerla hemos empleado el Teorema del seno además de las simplificaciones anteriormente mencionadas.

Sabemos también que el torque no es más que la primera derivada temporal del momento angular, y aproximando la órbita lunar a una circunferencia:

Introduciendo (1) en (2):

Y finalmente integrando:

Lo que, según la tasa actual de separación, implica que la Luna y la Tierra se alejan 3,4 cm cada año. Esa tasa se va frenando hasta el punto en que, cuando la variación de momento angular de la Luna se anule, sea cero. En ese instante desaparecerán las fuerzas de marea y la Tierra rotará a la misma velocidad a la que la Luna orbita nuestro planeta. Ambos periodos serán de 46 días.

Finalmente, hay que tener en cuenta que la energía del sistema se pierde debido a la viscosidad del agua en forma de calor. Una buena aproximación es que un 10% de la energía de subida del nivel del mar en una marea se disipa. Sabiendo aprovechar esta pérdida, podríamos producir en un año el equivalente a 10 mil millones de barriles de petróleo, la tercera parte de la energía consumida anualmente a nivel planetario. Yo creo que es una buena excusa para invertir en este tipo de energías.

Si quieres avanzar más y saber cómo se producen las mareas, haz clic aquí.

¡Un saludo y hasta la próxima!

El efecto Hall

Edwin Herbert Hall (1855-1938) fue un físico estadounidense que trabajó en Harvard, donde como estudiante de doctorado descubrió el efecto que lleva su nombre.

A grandes rasgos, el Efecto Hall consiste en la aparición de una diferencia de potencial eléctrico entre los extremos de un conductor atravesado por un campo magnético por el que circula una corriente.

Esquema ilustrativo del Efecto Hall

Imaginemos que nos encontramos en la década de 1870, cuando el Electromagnetismo es aún un gran desconocido. Todavía quedan muchos años para el descubrimiento del electrón (Thomson, 1897) y para la formulación de la Fuerza de Lorentz.

Las corrientes eléctricas eran un misterio, pero gracias al Efecto Hall se pudo saber que los portadores de carga que se desplazaban por los cables conductores eran negativos. Intentemos entenderlo desde el principio:

Sea un conductor plano de dimensiones transversales a y b recorrido por una intensidad I y atravesado por un campo magnético B, como se esquematiza en la ilustración inferior.

fig. 2

La fuerza de Lorentz aparece sobre cargas en movimiento en el interior de campos magnéticos, y el módulo de dicha fuerza es el producto del módulo del campo multiplicado por la velocidad y la carga (F = qvB). Su dirección es perpendicular a B y a v, y su sentido depende también de si la carga es positiva o negativa.

Es obvio que sobre las cargas que circulan por el conductor aparecerá una fuerza de Lorentz de sentido ascendente, de forma que los electrones (los portadores) se acumularán en la zona superior de la fig. 2, y que la zona inferior se cargará positivamente.

Como consecuencia de esa reordenación de las cargas, se formará un campo eléctrico uniforme que parte de la zona cargada positivamente hacia la zona cargada negativamente, de forma que tiende a anular la fuerza de Lorentz. Cuando el módulo de ambas fuerzas (magnética y eléctrica) sean iguales, aparecerá un voltaje constante en el tiempo llamado Voltaje Hall. De forma cuantitativa:

Una importante consecuencia de este efecto viene dada por el estudio del signo del voltaje observado. Veamos cómo se determinó que la carga de los portadores de corriente eléctrica (aún no se había descubierto el electrón) era negativa:

Como experimentalmente se determinó que el voltaje en B era menor que en A, el campo eléctrico estaba dirigido hacia arriba, y por consiguiente la fuerza de Lorentz tendría que dirigirse hacia abajo. De esta manera se supo que los portadores de corriente eléctrica poseían carga negativa.

Además de poder medir la carga del electrón, podemos usar el efecto Hall para medir la intensidad y el sentido de campos magnéticos, de corrientes eléctricas e incluso la densidad electrónica de materiales conductores y semiconductores. Se usa también en automovilismo, en música, en lectores de CD y en muchos más campos.

Sensor de proximidad basado en el Efecto Hall

Efecto Doppler Relativista

Antes de comenzar, recomiendo leer la entrada anterior (Fórmulas del Efecto Doppler). Gracias al Efecto Doppler se pudo comprobar la Expansión del Universo. En la entrada de hoy combinaremos lo de las tres últimas entradas con la Teoría de la Relatividad Especial de Albert Einstein.

En la entrada anterior hemos considerado el espacio y el tiempo como dimensiones aisladas y absolutas. ¿Pero qué pasa cuando la aproximación entre fuente y observador se aproxima a la velocidad de la luz? Tal y como habíamos dicho en la serie sobre Relatividad Especial, el espacio y el tiempo dependen uno del otro y no son absolutos, sino que dos observadores que se muevan a distintas velocidades pueden medir tiempos y espacios diferentes, y todo ello porque la velocidad de la luz es constante para cualquier observador. A físicos como Albert Einstein o Hendrik Lorentz le debemos estas maravillas.

Recordemos que la Teoría de la Relatividad nace de la idea de que la luz viaja siempre a la misma velocidad en el vacío, tal y como demostró el experimento de Milchelson y Morley.

Supongamos que fabricamos un reloj que funciona con un fotón (partícula asociada a la luz) que rebota entre dos espejos. Cuando rebota, va haciendo tic-tac, como en el del vídeo inferior.

Enlace desde móviles

La distancia d entre los dos espejos es igual a c·t, es decir, la velocidad de la luz por el tiempo que tarda en llegar de un espejo a otro. Dicho de otro modo, el tiempo es igual al espacio entre la velocidad: t = d/c.

Ahora supongamos que introducimos ese reloj en una nave espacial que se mueve a velocidad v. Un astronauta dentro de la nave seguirá oyendo esos tic-tac con la misma frecuencia, ¿pero cómo verá eso una persona desde la Tierra?

Enlace desde móviles

El fotón visto para un astronauta dentro de la nave, sube y baja en línea recta. Pero visto desde fuera, realiza un movimiento en zig-zag, como muestra la imagen inferior. Mediante una serie de sencillas operaciones, deducimos que el tiempo que medía el observador en movimiento (t) es inferior al que mide el observador en reposo (t'):

Eso significa que el tiempo transcurre relativamente más lento para una persona que se mueva que para una en reposo. Si alguien viajase por el espacio a una velocidad de 260.000 km/s durante 50 años, al volver a la Tierra parecería que solo ha envejecido 25 años. A velocidades pequeñas (coches, meteoritos, misiles...), esa dilatación temporal es imperceptible. Necesitaríamos viajar más de 5 millones de años sin parar en coche para que nuestro reloj se atrase solo 1 segundo...antes se queda sin pila...

Una vez repasada la dilatación temporal, podemos comenzar con nuestros típicos ejercicios de imaginación:

Imaginemos que una nave espacial que se mueve hacia nosotros con una velocidad v emite pulsos luminosos a ritmo constante. A nosotros nos interesa calcular la longitud de onda de esos pulsos, entonces contamos el número de ellos que suceden en un tiempo t, y también calculamos cuánto espacio recorre la nave en ese tiempo. Si llamamos N al número de pulsos contados en un intervalo de tiempo t, la longitud de onda será:

A partir de la longitud de onda, hallamos la frecuencia:

Según la Relatividad Especial, la imagen inferior relaciona el periodo medido desde el sistema de referencia del observador (T) y el de la fuente (T'). 

Combinando las ecuaciones (I) y (II), obtenemos:

Racionalizando la expresión superior y simplificándola:

Tenemos que recordar que según el Principio de Relatividad, el movimiento es relativo. Imaginemos que viajamos en coche. Según este principio, es equivalente decir que el coche se mueve respecto a la carretera que decir que la carretera se mueve debajo de las ruedas del coche. Por tanto, no podemos saber si es la fuente la que se mueve o si somos nosotros, solo podremos decir que existe un movimiento.

Dependiendo si fuente y observador se alejan o acercan entre sí, aquí quedan las fórmulas para la frecuencia y la longitud de onda:

Si aumenta la frecuencia, disminuye la longitud de onda y viceversa, ya que c es constante para cualquier sistema de referencia. Otra forma de ver las ecuaciones superiores es considerar positiva la velocidad cuando es de aproximamiento y negativa cuando se alejan, teniendo solo que usar la primera.

Dicho esto, solo nos queda aclarar lo dicho en la entrada sobre la Expansión del Universo.  

Si una estrella se aleja de nosotros, según las ecuaciones superiores, su frecuencia debería disminuir. Por eso mismo se produce el corrimiento al rojo, porque el rojo es el color de menos frecuencia del espectro visible. 

Por el contrario, si una estrella se acerca, se produciría el corrimiento al azul debido al mismo efecto.

Para terminar, un "problema-chiste": Un físico iba pensando en sus ecuaciones sobre la Teoría de Supercuerdas mientras conducía, como cualquier mañana normal. De repente se da cuenta de que le persigue la policía por saltarse un semáforo en rojo, pero como es físico, intenta pensar una escusa rápida. Le dice al policía que no vio el semáforo rojo, sino verde, debido al efecto Doppler. De todos modos, el agente le puso una multa por exceso de velocidad...¿A qué velocidad iba nuestro amigo el físico? Intenta calcularla y deja la respuesta en los comentarios. (La longitud de onda del rojo es de 650 nm y la del verde es de 520 nm). Este problema y su solución están en la sección Ingenio.

Demostración desde la matriz de Lorentz

La ecuación de onda electromagnética, en la imagen inferior, es una invariante relativista.

Luego la fase del campo eléctrico también ha de serlo. Definimos el cuadrivector K como:

Por lo que, en la dirección del movimiento tenemos que:

Y en direcciones perpendiculares a la del movimiento:

Y aquí acaba esta serie de 4 entradas sobre el Efecto Doppler. Si te ha gustado, no olvides compartir y dejar comentarios. Nos "vemos" en la próxima.

Un saludo!

Fórmulas del Efecto Doppler

En entradas anteriores (El Efecto Doppler y La Expansión del Universo) mencionamos una ecuación que nos permitía relacionar la frecuencia emitida (como el sonido "real" que sale de la sirena de una ambulancia) con la frecuencia percibida (sonido "distorsionado" que oímos). En la entrada de hoy vamos a intentar razonar por qué es así:

A. Observador en movimiento y fuente en reposo

El observador somos nosotros, los que percibimos, por ejemplo, un sonido. La fuente es el instrumento que emite ese sonido. Imaginemos un piano sonando y nosotros acercándonos hacia él. Las ondas que emite tienen una longitud de onda constante, pero al acercarnos, la frecuencia con la que nos llegan aumenta. Ahora intentaremos sacar una fórmula que relacione ambas frecuencias dependiendo de la velocidad con la que nos acerquemos (o alejemos):

Esta será la notación que usaremos en la entrada de hoy:

Como la longitud de onda no varía, igualaremos la longitud emitida con la percibida, y despejando obtendremos la ecuación encuadrada:

Cabe destacar que si el observador se aleja de la fuente, el signo "+" del numerador se transforma en un "-", por lo que la frecuencia al alejarnos de un sonido disminuirá y al acercarnos, aumentará.

B. Fuente en movimiento y observador en reposo

Si la fuente se aleja respecto a nosotros, cada pulso nos llega desde más lejos que el anterior, por lo que la longitud de onda aumentará de esta forma:

En el caso de que la fuente se acerque, la longitud de onda disminuiría, por tanto la frecuencia aumentaría y en el denominador de la fórmula encuadrada superior habría que poner un "-" en vez de un "+".

Fórmula General

Vamos a deducir una fórmula general en el caso de que tanto fuente como observador estén en movimiento.

Y como es lógico, combinándolas todas obtenemos la general:

El signo del numerador será "+" cuando el observador se acerque a la fuente, y "-" cuando se aleje. El signo del denominador será "-" cuando la fuente se acerque al observador y "+" cuando se aleje.

En la próxima entrada hablaremos sobre el Efecto Doppler Relativista. 

Hasta entonces! Y no os olvidéis de compartir y comentar ;)

La expansión del Universo

En las primeras décadas del siglo XX ya se conocían muy bien los espectros de emisión de los diferentes elementos. Un espectro de emisión es el conjunto de longitudes de onda que emite un elemento cuando uno de sus electrones disminuye de orbital, tal y como podéis recordar en mi entrada sobre las Auroras Polares.

Podemos imaginar que un electrón de un átomo es un libro. Podemos subirlo de estante o bajarlo, y al hacerlo, emite o absorbe energía. Un ejemplo son los fuegos artificiales de colores, hechos con elementos cuyos espectros se corresponden con los colores de la pirotecnia.

El color verde se consigue gracias al Bario

En esta página encontraréis los espectros de todos los elementos de la tabla periódica.

Como el Sol está formado por diversos elementos, si descomponemos su luz en colores podremos obtener en qué longitudes emite y por tanto sus elementos constituyentes, ya que cada elemento emite unas longitudes de onda correspondientes y bien definidas, tal y como establece el modelo atómico de Bohr.

Lo que hizo Edwin Hubble en la primera mitad del siglo XX es comparar el espectro del Sol (el Sol ni se aleja ni se acerca de nosotros) con el de un tipo especial de estrellas llamadas cefeidas. Estas estrellas tienen un brillo característico y regular, como un faro. Si conocemos su brillo, podemos saber la distancia a la que se encuentra, porque cuanto más lejos esté, menos brillará. 

La luz que emite el Sol es la de la izquierda, y la de una cefeida, la de la derecha. Se puede observar que las líneas negras están más hacia arriba en la cefeida que en el Sol, el conocido corrimiento al rojo. Esto, tal y como vimos en la entrada del Efecto Doppler, significa que esa cefeida se aleja de nosotros, al igual que la galaxia que la contiene. Como se aleja, las ondas que nos llegan de ella cada vez recorren más espacio, lo que se traduce como un aumento de la longitud de onda, que es lo que vemos comparando los espectros.

Hubble comparó el espectro de muchas cefeidas con el del Sol, y desarrolló la famosa ley de Hubble. Esta ley dice que cuanto más lejos está una galaxia, más rápidamente se aleja de nosotros. La desarrolló viendo cómo cambiaban los espectros entre unas cefeidas más cercanas y otras más lejanas, ya que el grado de corrimiento al rojo es proporcional a la distancia que nos separa de la cefeida.

En términos matemáticos, la ley dice que D = v/H, donde D es la distancia, v la velocidad de alejamiento y H es la constante de Hubble (H = 2,5·10E-18 Hz). Esa fórmula implica que cuanto más lejos está la galaxia, más rápido se aleja.

Y lo más importante es que todas las galaxias se alejan las unas de las otras entre sí, igual que los puntitos del globo de la imagen de abajo cuando la niña lo infla:

Cuando Hubble descubrió que el Universo se expandía aceleradamente, surgieron bastantes cuestiones: ¿Qué hace que se expanda? Y si cada vez es más grande, antes debió ser más pequeño. ¿Qué hubo al principio? ¿Cómo será el fin de nuestro Universo? 

Todas estas cuestiones las intentan responder los físicos cada día en laboratorios, aceleradores de partículas como el CERN o mediante la física teórica. Hablaremos de ellos en entradas posteriores. 

Para conocer más sobre cómo sabemos que el Universo está expansión, visita la entrada del Efecto Doppler Relativista.

Un saludo!

Crear materia a partir de luz

Sí, parece raro afirmar que a partir de algo sin masa como es la luz, podamos crear materia...

Recordando lo dicho en mi última entrada, la energía y la masa son magnitudes muy relacionadas. La ecuación simplificada que utilizaremos para ejemplificar esta situación es:

En la ecuación superior, la E hace referencia a la energía, la m a la masa y la c a una constante que es la velocidad de la luz en el vacío (aprox. 300.000.000 m/s).

Para una 'pequeña' masa de 1 kg, equivaldría una energía de 90.000.000.000.000.000 Julios, es decir, que si lográsemos transformar un solo kilo de masa en energía podríamos mantener encendida una bombilla convencional de 50W durante 57 millones de años...imagínate la energía que produce el Sol transformando cada segundo 4 millones de toneladas de materia en energía mediante la fusión nuclear. 

Más increíble aún, con la masa de un grano de arroz transformada íntegramente en energía, podríamos hacer que un coche de 1000 kg que está parado acelere hasta unos supuestos 420.000 km/h (hipotéticamente, ya que violaría la Teoría de la Relatividad de Einstein), o que un camión cargado con mil coches acelerara hasta 1000 km/h...y sólo con un grano de arroz...

Otro ejemplo es una bomba atómica, mediante la cual con pequeñas masas se pueden crear energías devastadoras. Einstein nos dejó una ecuación, conocimiento, pero no la forma de transformar materia en energía o viceversa.

El ejemplo de la bombilla y el del grano de arroz son solamente ejemplos. Hoy en día no sabemos cómo transformar la masa en energía útil con esas finalidades.

A lo largo del siglo XX numerosos físicos han tenido ideas sobre cómo hacerlo, algunas de las cuales se reflejan en los siguientes diagramas de Feynman (representaciones simbólicas de interacciones cuánticas):

Las más conocidas son la aniquilación de Dirac (donde un electrón y su antipartícula, el positrón, se aniquilan formando energía) y el efecto fotoeléctrico (donde un haz de fotones "arranca" electrones en una placa metálica, base teórica de la energía fotoeléctrica).

Los físicos Breit y Wheeler encontraron teóricamente que realizando el proceso inverso a la aniquilación de Dirac, se podrían generar electrones y positrones a partir de fotones muy energéticos. Hasta la actualidad, la tecnología no ha sido suficiente para demostrar su teoría, pero el pasado mes se logró idear el escenario necesario para tal experimento. ¿En qué consiste?

Primero, mediante un acelerador de partículas (un importante candidato sería el CERN de Ginebra), se aceleraría a velocidades próximas a la de la luz a un haz de electrones, que se harían colisionar contra oro para generar fotones muy energéticos. Después, harían incidir un rayo láser de alta energía contra una cavidad de oro para obtener temperaturas semejantes a las del Sol. Al igual que un hierro incandescente cambia de color al calentarse, la cavidad de oro a tan alta temperatura emitirá fotones muy energéticos, que se harían colisionar con el grupo anterior y así generar pares de electrones/positrones. La cavidad de oro funcionaría como un cuerpo negro, que emite ondas electromagnéticas a una frecuencia relacionada con su temperatura.

En todo momento se cumple que la energía total permanece constante, porque según la fórmula E=mc2, la energía de esos fotones ahora equivale a la masa del electrón más la del positrón.

Puede que en pocos años pueda realizarse este experimento, junto con la creación de grandes colisionadores de fotones. También puede que sea un paso más hacia la fusión fría, una rama de la física y de la tecnología que solventaría los problemas mundiales de energía.

Un saludo, espero que haya sido interesante.
Gabriel.