Crear materia a partir de luz

Sí, parece raro afirmar que a partir de algo sin masa como es la luz, podamos crear materia...

Recordando lo dicho en mi última entrada, la energía y la masa son magnitudes muy relacionadas. La ecuación simplificada que utilizaremos para ejemplificar esta situación es:

En la ecuación superior, la E hace referencia a la energía, la m a la masa y la c a una constante que es la velocidad de la luz en el vacío (aprox. 300.000.000 m/s).

Para una 'pequeña' masa de 1 kg, equivaldría una energía de 90.000.000.000.000.000 Julios, es decir, que si lográsemos transformar un solo kilo de masa en energía podríamos mantener encendida una bombilla convencional de 50W durante 57 millones de años...imagínate la energía que produce el Sol transformando cada segundo 4 millones de toneladas de materia en energía mediante la fusión nuclear. 

Más increíble aún, con la masa de un grano de arroz transformada íntegramente en energía, podríamos hacer que un coche de 1000 kg que está parado acelere hasta unos supuestos 420.000 km/h (hipotéticamente, ya que violaría la Teoría de la Relatividad de Einstein), o que un camión cargado con mil coches acelerara hasta 1000 km/h...y sólo con un grano de arroz...

Otro ejemplo es una bomba atómica, mediante la cual con pequeñas masas se pueden crear energías devastadoras. Einstein nos dejó una ecuación, conocimiento, pero no la forma de transformar materia en energía o viceversa.

El ejemplo de la bombilla y el del grano de arroz son solamente ejemplos. Hoy en día no sabemos cómo transformar la masa en energía útil con esas finalidades.

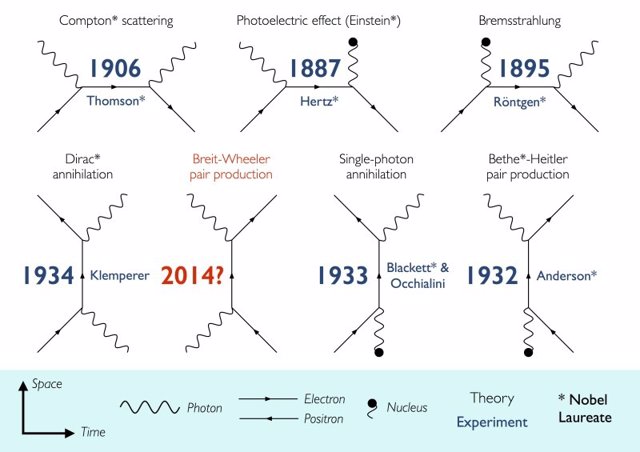
A lo largo del siglo XX numerosos físicos han tenido ideas sobre cómo hacerlo, algunas de las cuales se reflejan en los siguientes diagramas de Feynman (representaciones simbólicas de interacciones cuánticas):

Las más conocidas son la aniquilación de Dirac (donde un electrón y su antipartícula, el positrón, se aniquilan formando energía) y el efecto fotoeléctrico (donde un haz de fotones "arranca" electrones en una placa metálica, base teórica de la energía fotoeléctrica).

Los físicos Breit y Wheeler encontraron teóricamente que realizando el proceso inverso a la aniquilación de Dirac, se podrían generar electrones y positrones a partir de fotones muy energéticos. Hasta la actualidad, la tecnología no ha sido suficiente para demostrar su teoría, pero el pasado mes se logró idear el escenario necesario para tal experimento. ¿En qué consiste?

Primero, mediante un acelerador de partículas (un importante candidato sería el CERN de Ginebra), se aceleraría a velocidades próximas a la de la luz a un haz de electrones, que se harían colisionar contra oro para generar fotones muy energéticos. Después, harían incidir un rayo láser de alta energía contra una cavidad de oro para obtener temperaturas semejantes a las del Sol. Al igual que un hierro incandescente cambia de color al calentarse, la cavidad de oro a tan alta temperatura emitirá fotones muy energéticos, que se harían colisionar con el grupo anterior y así generar pares de electrones/positrones. La cavidad de oro funcionaría como un cuerpo negro, que emite ondas electromagnéticas a una frecuencia relacionada con su temperatura.

En todo momento se cumple que la energía total permanece constante, porque según la fórmula E=mc2, la energía de esos fotones ahora equivale a la masa del electrón más la del positrón.

Puede que en pocos años pueda realizarse este experimento, junto con la creación de grandes colisionadores de fotones. También puede que sea un paso más hacia la fusión fría, una rama de la física y de la tecnología que solventaría los problemas mundiales de energía.

Un saludo, espero que haya sido interesante.
Gabriel.

Dilatación Temporal

En la entrada anterior comencé una serie dedicada a la Relatividad Especial. Puedes leerla aquí: Introducción. En ella expliqué los antecedentes de la teoría, centrándome en el experimento de Milchelson y Morley, en el que demostraron que la velocidad de la luz en el vacío, c, era constante. Esta afirmación la introdujo Einstein en sus postulados, de la que deduciremos fenómenos sorprendentes. Hoy nos centraremos en cómo cambia la percepción del tiempo para dos observadores que se mueven a velocidades distintas.

A quien mucho le debemos en el mundo de la física es a H. A. Lorentz. Lo que nos incumbe hoy son sus transformaciones, ecuaciones matemáticas que relacionan el espacio y el tiempo dependiendo de la velocidad. A partir de ellas, deducimos que el tiempo se relantiza a medida que nos movemos más y más rápido, según esta ecuación simplificada:

t' = t·ß, donde ß es un factor que disminuye con la velocidad, t es el tiempo que mide el observador que está en reposo y t' el tiempo que mide el observador en movimiento.

Si quieres la dmostración de esta fórmula de manera sencilla, clic aquí.

A velocidades cotidianas (andar, correr, un coche, un avión o incluso una nave espacial), ß vale 1 o muy próximo a 1, conque el tiempo para una persona en reposo y otra dentro, por ejemplo, de un coche, es el mismo. Pero a medida que nos aproximamos a c, ß cada vez vale menos, tendiendo a 0. De aquí se deduce, por ejemplo, que mientras para una persona en la Tierra pasan 10 años, para una persona que hipotéticamente se moviese a un 87% de la velocidad de la luz, pasarían 5 años. Obviamente, esto es una forma de viajar en el tiempo hacia el futuro, más rápido de lo que lo estamos haciendo ahora, segundo a segundo. Para el viajero, el experimento de moverse tan rápido supondría un viaje en el tiempo hacia el futuro.

Pero, ¿cómo podemos entender esto fuera de las matemáticas?

Imagina que tenemos dos relojes formados cada uno por dos espejos uno enfrente del otro, tal y como muestra la imagen superior. Entre ellos hay un fotón que se mueve a la velocidad de la luz, rebotando de uno a otro. Cada vez que rebota, suena un "tic" que nos permite medir el tiempo. 

Si movemos uno de los dos relojes de izquierda a derecha, como en la figura superior, el fotón tardará más en alcanzar el espejo, porque como hemos dicho, no se puede superar la velocidad de la luz. El tiempo que tarde en rebotar dependerá de la velocidad a la que se mueva el reloj, ya que c es constante. Un reloj en reposo y otro en movimiento marcan tiempos diferentes. Lo entenderemos mejor en el siguiente vídeo:

Documental completo aquí.

Ahora traduciremos esto a lo que ocurriría en nuestro cuerpo o en cualquier objeto a esas velocidades: las interacciones electromagnéticas entre nuestros átomos, al igual que gran variedad de fenómenos, suceden a la velocidad de la luz. A grandes velocidades, estos procesos se ralentizarían tal y como hemos visto en el vídeo, lo que supondría esa dilatación temporal.

Si por algún casual pudiésemos viajar a la velocidad de la luz, algo imposible como veremos en entradas sucesivas, el fotón de nuestro reloj nunca alcanzaría el otro espejo porque se alejaría de él a su misma velocidad. De este modo, cualquier persona parada que nos observase nos vería congelados en el tiempo, al igual que para nosotros, él sería el que estaría "congelado".

La dilatación del tiempo se ha medido y demostrado experimentalmente. Se ha comprobado el retraso que sufren algunos relojes atómicos durante un viaje en avión respecto a otros que han permanecido quietos. La diferencia temporal es de pocos nanosegundos debido a la escasa velocidad de un avión en escalas relativistas.

Otro ejemplo es la desintegración de muones relativistas. Un muón es una partícula subatómica de la familia de los leptones, al igual que el electrón, con una carga negativa pero más masa que el electrón. Se desintegra en dos microsegundos, produciéndose un electrón y dos neutrinos. En grandes aceleradores de partículas como el LHC, donde consiguen acelerar muones a velocidades próximas a c, se ha comprobado que la vida media de estas partículas aumenta. Este fenómeno se puede explicar mediante la dilatación temporal que sufren a esas velocidades.

Otro dato sobre los muones: podemos detectar muones que nos llegan de capas altas de la atmósfera, pero con esa vida media no deberían recorrer ni un kilómetro...la única explicación razonable es esa dilatación temporal que sufren a esa enorme velocidad, que les aumenta la vida media y consiguen recorrer más espacio (que a su vez se contrae, como ya veremos).

Ahora bien, Antonio y Juan son dos gemelos. A la edad de 20 años, Antonio se embarca a bordo de una travesía espacial a un 95% de la velocidad de la luz. Medido en años terrestres, el viaje dura 60 años. Para Juan, su hermano en la nave viaja tan rápido que el tiempo deberá transcurrir para él más lento. De este modo, al volver, Antonio regresaría con 39 años mientras que Juan tendría 80. Pero para Antonio, que se encuentra en reposo en su nave, el que parece que se aleja de él es Juan, y al reencontrarse el anciano debería ser él y no su hermano, al contrario que antes. Solo uno tiene razón, ¿pero cuál?

Esta es la famosa paradoja de los gemelos, que dentro de dos entradas analizaremos y resolveremos, para ver quién de los dos tiene razón.

Y hasta aquí la entrada de hoy. Si te interesa la deducción matemática de la fórmula de la dilatación temporal, te animo a que sigas leyendo. En la próxima entrada trataré la contracción del espacio.

Las matemáticas de la dilatación temporal

Partiremos de las transformaciones de Lorentz tomándolas como verdaderas, de donde deduciremos la fórmula antes mencionada de la dilatación temporal.

Esta es la transformación de Lorentz que relaciona el tiempo en movimiento t' con el tiempo en reposo t.

El factor ß se calcula así: (c es la velocidad de la luz en el vacío y v es la velocidad del cuerpo en movimiento, que es constante)

Sustituímos ß en la ecuación de Lorentz:

El cuerpo en el eje cartesiano se desplaza a velocidad constante v:

Relación entre velocidad, espacio y tiempo: 

Sustituimos x en la ecuación de Lorentz y despejamos:

Hasta aquí hemos deducido la dilatación temporal t' = t·ß

En la imagen inferior deducimos que "en cada segundo, medido desde el sistema en reposo, el tiempo se retrasa (1-ß) segundos"

Espero que hayáis disfrutado con esta entrada, ya que yo lo he hecho escribiéndola. Dejad sugerencias y comentarios, y nos vemos en unos días con "La contracción del espacio".

Aceleradores de Partículas

Un acelerador de Partículas es una máquina capaz de hacer mover partículas a velocidades cercanas a la de la luz. Esto se consigue de diversas maneras, pero la más usual es mediante atracción y repulsión electrostática. Hay diversos tipos de aceleradores: los hay circulares, como el del CERN en Ginebra; y los hay lineales, como el que visité el verano pasado y dónde pasé una semana, del que voy a hablar.

¿Dónde se encuentra?

El acelerador se encuentra en Madrid, en la Universidad Autónoma. Pertenece al Centro de Microanálisis de Materiales. Se halla en un enorme edificio, con muros de hormigón de más de 1m de espesor, protegiendo la zona de cualquier peligro. Aquí podéis conocer más sobre este acelerador: Acelerador de Iones del CMAM.

¿Para qué sirve?

Su finalidad es el análisis de obras de arte, síntesis de nuevos materiales e investigación científica. En el caso de los circulares, su uso fundamental es el de colisionar partículas para conocer de qué está hecho todo. Gracias a ellos, en 2013 se demostró empíricamente la existencia del Campo de Higgs, postulado por Peter Higgs 50 años atrás. Otras veces para observar cómo fue el Universo en sus inicios. En posteriores entradas hablaré de este tema. En el de Madrid, el objetivo es bombardear con una haz de iones un material. Los iones se aceleran y dirigen hacia la muestra, y dependiendo de la intensidad de rebote, estaremos tratando con unos elementos u otros. Esta técnica, llamada RBS, es la más común.

Funcionamiento

Esquema de un acelerador lineal tipo tándem

El proceso comienza en la parte de la izquierda. Podemos observar dos fuentes de partículas, una para gases y otra para sólidos. Mediante distintas técnicas, arrancamos esas partículas y las ionizamos, es decir, las cargamos positiva o negativamente para poder atraerlas hacia la muestra.

Una vez ionizadas (normalmente se usa Cesio), mediante el uso de campos magnéticos, atraemos el haz de iones hacia la parte azul del dibujo. Aquí se ven atraídas por un voltaje de 5 millones de voltios hacia el centro del tanque. Una vez allí, mediante el uso de Nitrógeno, las cargamos positivamente, por lo que la fuerza que antes las atrajo, ahora las repele. De esta manera conseguimos acelerar nuestro haz a una velocidad de, aproximadamente, 10.000 km/s. Una vez que el haz sale de la zona pintada de rojo, lo desviamos mediante electroimanes de 4 polos y concentramos todas las partículas en un haz de una superficie como la de una moneda de 1 céntimo. Dirigimos el haz a la muestra, y mediante detectores conseguimos saber la relación en masas de las partículas que rebotan y las de la muestra. Así podemos saber de qué está hecho aquello que hemos bombardeado.

Tanque del acelerador

Una de las vías donde se depositan muestras para su análisis

En el interior del acelerador hay anillos, donde se aplica el voltaje deseado. Debido a esa gran cantidad de energía, es necesario ocupar el espacio entre esos anillos con un gas muy denso, a una presión de 7 atmósferas para evitar descargas eléctricas. El coste de mantener el acelerador funcionando 1 día es de más de 2000 €.

Análisis

Todos estos datos son llevados a un potente ordenador, aquí se grafican las energías de todos esos choques y rebotes. Son los llamados espectros. 

Pero aquí no acaba todo, ya que ahora viene la parte más difícil de todas: mediante distintos programas informáticos, hacemos una gráfica 'teórica' del espectro. En ese programa introducimos las sustancias que hemos usado de muestra, con sus porcentajes en masa de cada elemento. El programa simula lo que debería haber salido experimentalmente:

Construcción de un espectro

Los puntitos negros son los rebotes experimentales. La línea roja, lo que teóricamente debería haber salido.

El proceso de análisis de gráficas pude llevar horas y horas. Pude ser que algún elemento se haya oxidado, y salgan líneas en la gráfica que no deberían estar. 

Finalmente, cuando la línea teórica coincide con la real, podemos afirmar que hemos acabado nuestro trabajo.

Conclusión

El trabajo en un acelerador es muy variado. En el ejemplo de los lineales, se analizan muestras haciendo rebotar partículas en ellas. Con esos rebotes construimos una gráfica. Si la teórica coincide con la experimental, ya sabemos de qué está hacha nuestra muestra. Si no coincide, debemos modificar valores para ajustarla, ya que pueden haber reaccionado elementos, puede haber impurezas...

Durante esa semana que estuve en el acelerador, te acabas dando cuenta que ser científico no es estar en un laboratorio mezclando cosas, sino que es un trabajo laborioso, metódico y difícil. Trabajar como científico es duro, pero cuando consigues algo te das cuenta de que ese duro trabajo ha merecido la pena

Si te ha interesado el tema, en este enlace podrás ver un esquema del funcionamiento del acelerador, hecho por unos amigos y yo en el siguiente enlace: Prezi.

¿Qué pasaría si metemos la mano en un acelerador de partículas? 

La respuesta la encontrarás aquí: Peligros de un acelerador de partículas.

Cualquier duda, por favor, deja un comentario. La semana que viene volveré con un nuevo tema.

¡HASTA LA SEMANA QUE VIENE!