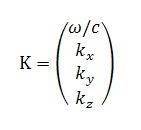Antes de comenzar, recomiendo leer la entrada anterior (Fórmulas del Efecto Doppler). Gracias al Efecto Doppler se pudo comprobar la Expansión del Universo. En la entrada de hoy combinaremos lo de las tres últimas entradas con la Teoría de la Relatividad Especial de Albert Einstein.
En la entrada anterior hemos considerado el espacio y el tiempo como dimensiones aisladas y absolutas. ¿Pero qué pasa cuando la aproximación entre fuente y observador se aproxima a la velocidad de la luz? Tal y como habíamos dicho en la serie sobre Relatividad Especial, el espacio y el tiempo dependen uno del otro y no son absolutos, sino que dos observadores que se muevan a distintas velocidades pueden medir tiempos y espacios diferentes, y todo ello porque la velocidad de la luz es constante para cualquier observador. A físicos como Albert Einstein o Hendrik Lorentz le debemos estas maravillas.
Recordemos que la Teoría de la Relatividad nace de la idea de que la luz viaja siempre a la misma velocidad en el vacío, tal y como demostró el experimento de Milchelson y Morley.
Supongamos que fabricamos un reloj que funciona con un fotón (partícula asociada a la luz) que rebota entre dos espejos. Cuando rebota, va haciendo tic-tac, como en el del vídeo inferior.
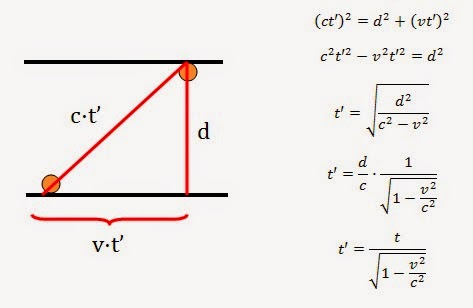
La distancia d entre los dos espejos es igual a c·t, es decir, la velocidad de la luz por el tiempo que tarda en llegar de un espejo a otro. Dicho de otro modo, el tiempo es igual al espacio entre la velocidad: t = d/c.
Ahora supongamos que introducimos ese reloj en una nave espacial que se mueve a velocidad v. Un astronauta dentro de la nave seguirá oyendo esos tic-tac con la misma frecuencia, ¿pero cómo verá eso una persona desde la Tierra?
El fotón visto para un astronauta dentro de la nave, sube y baja en línea recta. Pero visto desde fuera, realiza un movimiento en zig-zag, como muestra la imagen inferior. Mediante una serie de sencillas operaciones, deducimos que el tiempo que medía el observador en movimiento (t) es inferior al que mide el observador en reposo (t'):
Eso significa que el tiempo transcurre relativamente más lento para una persona que se mueva que para una en reposo. Si alguien viajase por el espacio a una velocidad de 260.000 km/s durante 50 años, al volver a la Tierra parecería que solo ha envejecido 25 años. A velocidades pequeñas (coches, meteoritos, misiles...), esa dilatación temporal es imperceptible. Necesitaríamos viajar más de 5 millones de años sin parar en coche para que nuestro reloj se atrase solo 1 segundo...antes se queda sin pila...
Una vez repasada la dilatación temporal, podemos comenzar con nuestros típicos ejercicios de imaginación:
Imaginemos que una nave espacial que se mueve hacia nosotros con una velocidad v emite pulsos luminosos a ritmo constante. A nosotros nos interesa calcular la longitud de onda de esos pulsos, entonces contamos el número de ellos que suceden en un tiempo t, y también calculamos cuánto espacio recorre la nave en ese tiempo. Si llamamos N al número de pulsos contados en un intervalo de tiempo t, la longitud de onda será:
A partir de la longitud de onda, hallamos la frecuencia:
Según la Relatividad Especial, la imagen inferior relaciona el periodo medido desde el sistema de referencia del observador (T) y el de la fuente (T').
Combinando las ecuaciones (I) y (II), obtenemos:
Racionalizando la expresión superior y simplificándola:
Tenemos que recordar que según el Principio de Relatividad, el movimiento es relativo. Imaginemos que viajamos en coche. Según este principio, es equivalente decir que el coche se mueve respecto a la carretera que decir que la carretera se mueve debajo de las ruedas del coche. Por tanto, no podemos saber si es la fuente la que se mueve o si somos nosotros, solo podremos decir que existe un movimiento.
Dependiendo si fuente y observador se alejan o acercan entre sí, aquí quedan las fórmulas para la frecuencia y la longitud de onda:
Si aumenta la frecuencia, disminuye la longitud de onda y viceversa, ya que c es constante para cualquier sistema de referencia. Otra forma de ver las ecuaciones superiores es considerar positiva la velocidad cuando es de aproximamiento y negativa cuando se alejan, teniendo solo que usar la primera.
Dicho esto, solo nos queda aclarar lo dicho en la entrada sobre la Expansión del Universo.
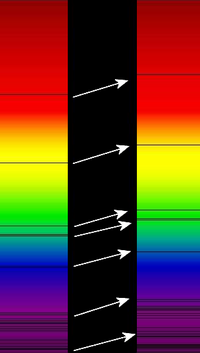
Si una estrella se aleja de nosotros, según las ecuaciones superiores, su frecuencia debería disminuir. Por eso mismo se produce el corrimiento al rojo, porque el rojo es el color de menos frecuencia del espectro visible.
Por el contrario, si una estrella se acerca, se produciría el corrimiento al azul debido al mismo efecto.
Para terminar, un "problema-chiste": Un físico iba pensando en sus ecuaciones sobre la Teoría de Supercuerdas mientras conducía, como cualquier mañana normal. De repente se da cuenta de que le persigue la policía por saltarse un semáforo en rojo, pero como es físico, intenta pensar una escusa rápida. Le dice al policía que no vio el semáforo rojo, sino verde, debido al efecto Doppler. De todos modos, el agente le puso una multa por exceso de velocidad...¿A qué velocidad iba nuestro amigo el físico? Intenta calcularla y deja la respuesta en los comentarios. (La longitud de onda del rojo es de 650 nm y la del verde es de 520 nm). Este problema y su solución están en la sección Ingenio.
Demostración desde la matriz de Lorentz
La ecuación de onda electromagnética, en la imagen inferior, es una invariante relativista.
Luego la fase del campo eléctrico también ha de serlo. Definimos el cuadrivector K como:
Por lo que, en la dirección del movimiento tenemos que:
Y en direcciones perpendiculares a la del movimiento:
Y aquí acaba esta serie de 4 entradas sobre el Efecto Doppler. Si te ha gustado, no olvides compartir y dejar comentarios. Nos "vemos" en la próxima.
Un saludo!