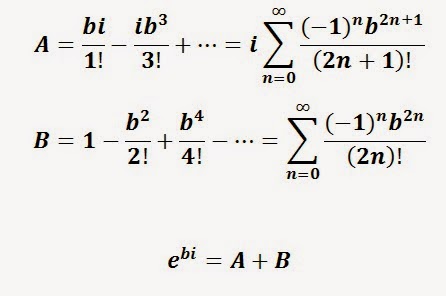La Igualdad de Euler

Leonhard Euler fue un matemático y físico suizo que vivió en el siglo XVIII. Es considerado uno de los grandes genios de la historia de la Ciencia. A él le debemos la existencia del número que lleva su nombre, el número e. Si quisiésemos hablar de todo lo que hizo, esta entrada se haría interminable, por lo que hoy me centraré en la famosa Ecuación de Euler:

Vamos a intentar demostrar esta identidad de gran belleza a partir de las Series de Taylor y Maclaurin, que son representaciones de una función (como el seno, el coseno o una exponencial) a partir de la suma de infinitos términos. Por ejemplo: sen 45º se puede escribir como la suma de infinitos sumandos que converge hacia el valor concreto del sen 45º. Las series que necesitaremos son las siguientes:

También necesitaremos algo de números complejos. Recordemos que un número complejo z puede escribirse como z = a + bi, siendo i la unidad imaginaria (raiz cuadrada de -1). Podemos escribir lo siguiente:

Ahora intentemos escribirlo mediante las Series de Taylor:

Podemos observar que hay algunos términos que poseen la unidad imaginaria i, pero otros no. Vamos a llamar A a la suma de los términos que incluyen i, y B a la suma de los que no:

Siendo un poco observadores, podemos escribir lo siguiente:

Ahora vamos a igualar b al número pi:

Con lo que queda demostrada la Identidad de Euler, dotada de una belleza espectacular y de misterio. Relaciona los cinco números básicos de las Matemáticas de una forma asombrosamente básica.

No sabemos cuál es su significado, pero sabemos que es verdad: una verdad eterna y bella, por lo que muchos la consideran la igualdad más importante de las Matemáticas.

Podemos tomar logaritmo neperiano a ambos lados y observar cuánto vale el logaritmo neperiano de -1:

Si os ha gustado la entrada matemática de hoy, os invito a comentar y compartirla. 

Un saludo, nos vemos en la próxima!

¡La Luna a 40 pasos!

¿Cuántas veces tenemos que doblar un folio para llegar a la Luna? La respuesta resultará increíble: 42.

Veremos ahora el porqué:

Un taco de 500 folios tiene un grosor de 5 cm aproximadamente. Si dividimos el grosor entre el número de folios, obtenemos que cada folio tiene un grosor de tan solo 0,1 mm.

Si doblamos por la mitad el folio, su grosor será el doble (0,2 mm); la segunda vez ya será 0,4 mm; la siguiente, 0,8 mm...y así sucesivamente, duplicándose el grosor en cada doblez:

Folio original: 0,1 mm

1ª Doblez: 0,1 · 2 mm

2ª Doblez: 0,1 · 2 · 2 mm

3ª Doblez: 0,1 · 2 · 2 · 2 mm

Así, cada vez que doblamos, multiplicamos por dos el grosor. En la doblez 10, el grosor será 2^10 veces mayor. Si observamos la siguiente tabla y su correspondiente gráfica, observamos cómo crece el grosor con respecto al número de veces que doblamos el folio:

Tabla de valores

Gráfica de la función

Nos encontramos ante un crecimiento exponencial. Aunque al principio el grosor aumente poco, a mediada que seguimos doblando aumenta muchísimo. Cuando lo doblamos x veces, su grosor será 2^x veces mayor.

La distancia media entre la Tierra y la Luna es de 384.400 Km. Ahora intentaremos expresar todo esto de forma matemática, sin olvidar de indicar todo en las mismas unidades. Igualaremos el grosor de la doblez nº X a la distancia entre la Tierra y la Luna, para así despejar la X y saber cuántas veces hay que doblar el papel.

Aplico el Cambio de Base para poder realizar la operación con mi calculadora.

Es decir, doblando un folio tan solo 42 veces...¡PODEMOS LLEGAR A LA LUNA!

Matemáticamente esto queda muy bonito, pero físicamente dudo que puedas llegar a doblar el folio más de 7 u 8 veces. Si se pudiese hacer, la superficie del folio sería muy inferior, exactamente 2^42 veces más pequeña. Es como si tuviésemos una superficie cuadrada de 1200 átomos de lado (unos pocos nanómetros cuadrados)...algo que a simple vista es imposible contemplar.

Aplicando los mismos pasos, y conociendo la distancia al Sol (149.600.000 Km) tenemos que el número de veces que necesitamos doblar un folio es aproximadamente 50 (50,4 exactamente).

¡Para llegar al Sol, solo tendríamos que doblar el folio 8 veces más!

Y más sorprendente aún, mediante el mismo procedimiento solo tendríamos que doblar un folio 81 veces para llegar al centro de la Galaxia...y solamente dos veces más para llegar de punta a punta de ella...¡INCREÍBLE!

Intentad doblar un folio 42 veces y dejáis en los comentarios qué tal vuestro paseo lunar. Dejad también en los comentarios temas para mi siguiente entrada que intentaré publicar este fin de semana. Tengo pensado preparar algo chulo sobre Relatividad, pero lo dejaré para dentro de una o dos semanas, así que proponed ideas.

Un Saludo Científicos,

HASTA OTRA!