Para concluir esta triada de entradas relacionadas con las mareas, hoy hablaré de la explicación física de las propias mareas. Las otras dos publicaciones son El Efecto Marea y los Corales y la duración del día.
La relación entre las aceleraciones de dos sistemas, uno inercial y el otro no inercial, se halla así:
La relación entre las aceleraciones de dos sistemas, uno inercial y el otro no inercial, se halla así:
Ahora esquematicemos el sistema Tierra-Luna:
Sea una masa m localizada en la superficie terrestre. Por simplicidad, consideremos que la Tierra no gira sobre su eje y que la hidrosfera recubre toda la superficie del planeta. La masa solo está afectada gravitacionalmente por la Tierra y la Luna, de momento. La segunda ley de Newton sobre esta masa desde el sistema centro de masas nos permite escribir:
Donde E es el empuje hidrostático y el vector a se refiere al sistema centro de masas.
Como consideramos la masa estática desde el sistema Tierra (despreciamos efecto Coriolis), así como que exista vector rotación ni su primera derivada temporal, en la ecuación deducida de (1) solo nos queda:
Donde el vector radio estrella es el que va desde el CM del sistema Tierra-Luna al centro de la Tierra. Como decíamos, por Newton podíamos escribir:
Siendo el vector F el que compensa a E para que la masa m esté en reposo. Sabiendo que la distancia entre la Tierra y el centro de masas del sistema es:
Y aplicando la Ley de la Gravitación de Newton podemos hallar la velocidad angular tal que:
Podemos decir, finalmente, que la fuerza F es:
Si nos fijamos, el primer término es simplemente la atracción terrestre. Teniendo solo en cuenta este primer término, no se producirían las mareas, por lo que el segundo y el tercer miembro de la ecuación son los generadores de mareas. De este modo llamamos f a la fuerza generadora de mareas de forma que:
Un esquema ilustrativo sobre nuestro planeta podría ser el siguiente:
Ahora procedamos a calcular cuál es el tiempo que transcurre entre dos mareas. Aparentemente puede parecer que son 12h, es decir, dos pleamares y dos bajamares diarias, pero mientras gira la Tierra sobre su eje, la Luna ha recorrido un pequeño ángulo de su órbita, variando la posición del centro de masas.
En la figura superior, las mareas altas se producen en la línea que une los centros de la Tierra y la Luna. En un instante inicial, nos encontramos en el punto A'. Queremos hallar el tiempo que transcurre hasta que nos encontremos en A. Como, desde la Tierra, el CM gira a la misma velocidad angular que la Luna, nuestra posición angular respecto al centro de la Tierra y la posición del punto A son, respectivamente,
Resolviendo el sistema obtenemos que el periodo T de las mareas es:
Podemos ver en la siguiente página una Tabla con las mareas de Gran Canaria. Como observamos, hay pequeás variaciones de minutos por las aproximaciones y simplificaciones hechas, además de por no tener en cuenta el liger efecto del Sol.
Para concluir la entrada, os dejo un vídeo ilustrativo que resume un poco todo.
Un saludo!






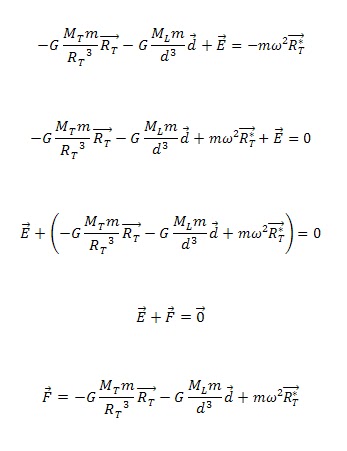







Muy Bueno!
ResponderEliminarMuy bien y muy ilustrativo
ResponderEliminar