Están en multitud de edificios o naves industriales, en forma de tubo, bombilla enrollada, etc. ¿Pero cómo funcionan? En la entrada de hoy hablaremos del funcionamiento y fundamento físico de las famosas lámparas fluorescentes, sus características y propiedades más relevantes. Para ello nos centraremos solamente en los tubos.
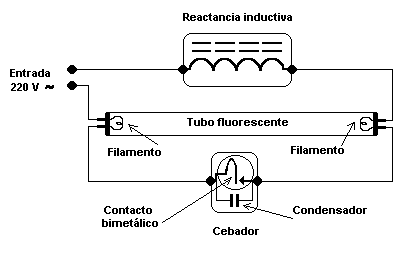
Un tubo fluorescente está formado, básicamente, por tres piezas: el tubo en sí, un cebador y una reactancia inductiva. El tubo es de vidrio, y en su interior se halla el vapor de mercurio combinado con algún gas inerte como el neón o el argón. Recubriendo el cristal hay un material llamado "fósforo", aunque no contenga esta sustancia. Su misión es absorber la luz UV que emite el mercurio al desexcitarse y emitir luz visible. Un tubo fluorescente sin este recubrimiento sería una lámpara de "luz negra".
 |
| Fuente: Wikipedia |
Conectado al tubo hay un cebador. Se trata de un dispositivo con una ampolla de vidrio que contiene gases (como neón o argón) que al conectarse a la corriente se calientan y expanden. Dicha expansión cierra un circuito que hace que los filamentos del tubo (generalmente wolframio) se calienten al rojo vivo y comiencen a ionizar los gases del interior del tubo. Es en este momento cuando aparece ese color anaranjado en los extremos de los tubos antes de encenderse.
Al cerrarse el circuito del cebador, el gas se enfría, se contrae y se abre bruscamente el circuito. Es ahora cuando entra en juego la reactancia. De acuerdo con la ley de Faraday, la fuerza electromotriz inducida (o fem) es igual a la variación del flujo magnético, sin olvidar un signo menos:
$\text{fem}=-\displaystyle\frac{d\Phi_{B}}{dt}$
La reactancia no es más que un solenoide o inductancia por el que circula la corriente. Por la Ley de Ampère, dentro de dicho solenoide aparecerá un campo magnético $\vec{B}$. Al cerrarse bruscamente el circuito, habrá una gran variación de flujo, y por efecto de autoinducción se inducirá una elevada fuerza electromotriz (de miles de voltios) que terminará de ionizar los gases del tubo. Una vez ocurrido esto, se establece una corriente de electrones entre el cátodo y el ánodo del tubo sin necesidad de altos voltajes.
Debido a que en Europa la corriente alterna oscila con una frecuencia de 50 Hz, los fluorescentes "parpadean" 100 veces cada segundo. Para evitar estos efectos estreboscópicos hay varias opciones. Una de ellas es la incorporación de un alternador electrónico que aumente dicha frecuencia a 50.000 Hz, como en las modernas bombillas fluorescentes. Otras opciones pueden ser colocar varios tubos juntos con corrientes desfasadas, minimizándose este efecto.
El consumo de un tubo fluorescente, así como su rendimiento, es bastante bajo. En la imagen inferior podemos observar el espectro emitido por una lámpara fluorescente de vapor de mercurio.
Como vemos, muy poca luz se desperdicia como infrarrojos, de modo que casi la totalidad de la potencia consumida se aprovecha para iluminación.
Asimismo, la potencia de los tubos es generalmente muy baja. Su pico de máximo consumo se alcanza al encender, pues es cuando más voltaje consume para ionizar el gas de mercurio. Es por eso por lo que se recomienda utilizar estas lámparas en lugares donde se necesite una fuente de luz permanente, es decir, que no se apaguen y se enciendan muchas veces. Esto también es porque la vida útil de las lámparas decrece cuantas más veces se enciendan.
Por último explicaremos por qué es necesario un condensador en este tipo de lámparas, para lo cual tendremos que introducir el concepto de potencia efectiva. Como sabemos, la corriente que llega a nuestras casas es alterna, es decir, oscilante. El motivo es simplemente las ventajas a la hora de transportarla. Por tanto, el voltaje que llega a nuestros enchufes (220 V en España) es oscilante. Entonces, ¿por qué un multímetro marca 220 V y no oscila? La respuesta es que lo que marca el multímetro no es el voltaje "instantáneo", sino el "eficaz", una especie de promedio.
La potencia que consumimos también se mide de esta forma promediada. Al manejar las ecuaciones se llega a que la potencia "activa" depende de un factor de potencia que va desde 0 hasta 1. Ese factor no es más que el coseno del desfase entre la intensidad y el voltaje. Como nos interesa que el factor de potencia esté lo más próximo a 1 posible, necesitamos conseguir una resonancia entre reactancia inductiva y capacitiva. Será más fácil si observamos matemáticamente el desfase $\phi$:
$\phi=\arctan\displaystyle\frac{L\omega-1/C\omega}{R}$
Para hacer que el factor de potencia sea 1, hay que hacer que $\phi$ sea cero, para lo cual hay que colocar un condensador de capacidad $C$ tal que a la frecuencia $\omega$ de la red eléctrica, compense la inductancia $L$ de la reactancia del fluorescente.
Espero que os haya gustado la breve entrada de hoy. Un saludo!



