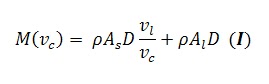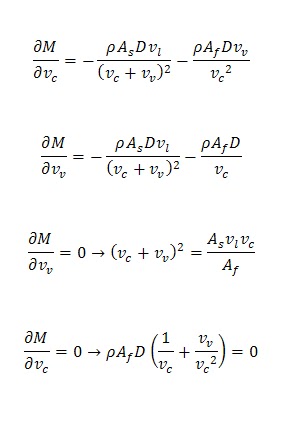Probablemente lo primero que hagas sea sacar un paraguas, sobre todo si eres precavido, pero si no dispones de uno, ¿qué es mejor para mojarse menos: correr o andar?
Aproximemos el cuerpo humano a un paralelepípedo de área frontal Af y área superior As como se muestra en la figura inferior. No es una mala aproximación si pensamos en As como la suma del área de la cabeza y los hombros y Af como la suma de cara, torso, brazos y piernas.
Ahora planteemos el problema:
Nuestro amigo el paralelepípedo se encuentra a una distancia D de su destino y quiere llegar a él mojándose lo menos posible. Para evitar mojarse, puede desplazarse con la velocidad que desee y puede inclinar su cuerpo si lo cree conveniente. También puede agacharse con el consiguiente detrimento de su velocidad.
Algunas consideraciones:
-La masa de todas las gotas de lluvia es la misma.
-La concentración de gotas de lluvia por unidad de volumen es constante en todo el recorrido.
-La densidad del agua es constante.
-La velocidad y dirección del viento es invariante durante todo el trayecto.
-La velocidad de caída de la lluvia, así como la del corredor es constante.
-Las gotas han alcanzado todas su velocidad límite por la fricción con el aire.
Problema:
Manera óptima para mojarse lo menos posible. Buscar una función del total de agua caída sobre el cuerpo para minimizarla, si es posible.
Caso #1 Sin viento
Sea Vc la velocidad del corredor y Vl la velocidad de la lluvia. Desde el sistema de referencia del sujeto, el experimento se vería así:
Podemos ver que el agua que caerá sobre la cabeza y los hombros será menor cuanta mayor sea la velocidad. Para calcular dicha masa de agua, basta con considerar la cantidad encerrada en la columna de agua de base As o Al y cuya altura dependerá obviamente de D.
Sin tener en cuenta que el corredor pueda agacharse o inclinarse, llegamos a que la cantidad de agua M que cae sobre el sujeto en función del cociente entre Vc y Vl es:
Al derivarla obtenemos una función decreciente con una asíntota horizontal, ya que efectivamente al observar la gráfica de M vemos que:
Lo que evidentemente nos lleva a pensar que es una función monótomamente decreciente en el intervalo que nos interesa (desde que Vc es 0 hasta que tiende a infinito).
Las dos soluciones válidas para que te mojes lo menos posible son:
-Ir a la máxima velocidad posible, pero te mojas una cantidad fija (la columna frontal).
-Que la velocidad de la lluvia sea 0, es decir, que no llueva...
 |
| Masa de agua (eje azul) en función de la velocidad de la lluvia (eje verde) y de la velocidad del corredor (eje rojo) |
Por consiguiente, en ausencia de viento y a velocidad arbitraria, te mojas menos cuanto más rápido vayas y cuanto menor sea la velocidad de la lluvia.
Consideraremos la velocidad vertical de la lluvia como constante. Efectivamente, la ecuación del movimiento de una gota de lluvia será:
Y considerando la segunda derivada como nula, obtenemos el valor de la velocidad límite
Que en condiciones normales oscila entre los 15 y los 35 km/h.
Podemos considerar ahora que el corredor se incline hacia delante un ángulo delta. La forma de minimizar el agua que impacta con su cuerpo es hacer que el ángulo de inclinación sea, evidentemente, theta. De este modo obtenemos:
La expresión corresponde a la cantidad de agua sobre la cabeza, que obviamente tiende a infinito cuando se está parado, y tiende a una cantidad fija cuando la velocidad del corredor tiende a infinito.
Si graficamos esta función obtenemos:
Como es obvio, la cantidad de agua tiende a una constante, que no es ni más ni menos que el coeficiente de la raíz.
En caso de considerar variable la velocidad del agua:
 |
Masa de agua (eje azul) en función de la velocidad de la lluvia (eje verde)
y de la velocidad del corredor (eje rojo)
|
Ahora comparemos la masa de agua del corredor sin inclinarse (I) y la del que se inclina (II):
Llamaremos beta al cociente entre la velocidad de la lluvia y la del corredor. Si restamos a la ecuación (II) a la (I), obtenemos:
Por consiguiente, existen ciertos valores de beta para los cuales es preferible correr recto a correr inclinado. Basta con resolver la ecuación superior cuando delta de M es cero, y obtenemos precisamente la condición para la cual es conveniente no inclinarse:
Asimismo, como beta va a ser siempre positivo ya que las velocidades lo son, el cociente tendrá que ser mayor que cero también, para lo cual el área de la cabeza debería ser mayor que el área frontal, cosa que en una persona no ocurre, pero sí en otros animales.
De esta forma llegamos a que es preferible inclinarse siempre en la dirección del desplazamiento.
La inclinación óptima será, lógicamente, aquella que coincida con el ángulo que forman las componentes de la velocidad de la lluvia. Esto se debe a que la cantidad de agua en función del ángulo de inclinación tiene un mínimo cuando ese ángulo es theta.
Caso #2 Con viento
Ahora consideremos que nos da el viento a velocidad constante en la dirección de la trayectoria. En la suma vectorial de las velocidades tenemos que incluir la velocidad del viento y obtenemos, tanto para viento de cara como para viento de espalda:
Es fácil de observar que, a parte de todo lo dicho con anterioridad, la velocidad del viento influye, ya que aumenta lo que te mojas frontalmente. Considerando constante la velocidad de caída de la lluvia y haciendo la gráfica M (Vc, Vv):
 |
| Observamos que cuando Vc = -Vv, M es mínimo |
Efectivamente cuando el viento nos da de espalda y nos movemos a la misma velocidad, desde nuestro sistema de referencia el agua nos cae sobre la cabeza y es mínima. Esa cantidad de agua es, precisamente:
Aunque sea trivial, tratemos de demostrar que la velocidad óptima es igual a la velocidad del viento de espaldas:
Y al resolver esa última ecuación se obtiene
Que es la solución obvia que antes habíamos indicado.
También podemos optar por inclinarnos un ángulo theta. El ángulo óptimo de inclinación, en este caso, sería:
Que evidentemente, cuando Vc = -Vv, ese ángulo es cero. Al inclinarse ese ángulo, el problema se reduce únicamente al agua que cae sobre la cabeza y los hombros.
Es lógico que por culpa del viento el corredor va a verse frenado, lo que aumentaría la pendiente de mojado, pero lo omitiremos por simplicidad.
Está claro que es preferible inclinarse a no hacerlo, pero a altas velocidades no es posible por las limitaciones del cuerpo humano. Por ello podemos pensar: ¿es preferible correr a la velocidad del viento o correr muy rápido? ¿Cómo te mojas menos?
Si hacemos tender la velocidad a valores altos, podemos despreciar el primer sumando y obtenemos que el agua caída sobre el cuerpo es aproximadamente
Si, por el contrario optamos por correr a la velocidad del viento, la masa sería
Comparando las dos expresiones, podemos ver que Mo es del mismo orden que M, pero menor. Además hay que tener en cuenta que M es más grande, ya que hemos prescindido del primer sumando.
Por todo ello, es preferible correr despacio a la velocidad del viento que no muy rápido cuando el viento te viene de espalda.
Conclusiones
- En ausencia de viento, es preferible correr a la máxima velocidad posible.
- En ausencia de viento, lo óptimo es inclinarse en la dirección del desplazamiento un ángulo que coincida con el de la lluvia (desde tu sistema de referencia)
- Con viento de cara, es aconsejable inclinarse hacia delante en el ángulo en el que caiga la lluvia.
- Con viento de espalda, lo preferible es correr a la velocidad del viento.
- Si el viento es lateral, descomponerlo en sus componentes y aplicar una de las dos conclusiones superiores, pero a la máxima velocidad posible.
Para concluir la entrada, os dejo un vídeo del genial Walter Lewin, ex-profesor emérito del Massachusetts Institute of Technology (MIT), donde habla de este problema.
Un saludo y hasta la próxima.
Recordad comentar y compartir!
- En ausencia de viento, es preferible correr a la máxima velocidad posible.
- En ausencia de viento, lo óptimo es inclinarse en la dirección del desplazamiento un ángulo que coincida con el de la lluvia (desde tu sistema de referencia)
- Con viento de cara, es aconsejable inclinarse hacia delante en el ángulo en el que caiga la lluvia.
- Con viento de espalda, lo preferible es correr a la velocidad del viento.
- Si el viento es lateral, descomponerlo en sus componentes y aplicar una de las dos conclusiones superiores, pero a la máxima velocidad posible.
Para concluir la entrada, os dejo un vídeo del genial Walter Lewin, ex-profesor emérito del Massachusetts Institute of Technology (MIT), donde habla de este problema.
Un saludo y hasta la próxima.
Recordad comentar y compartir!