El objetivo de esta sección es meramente de ocio. Cada semana propondré un nuevo acertijo relacionado con física, lógica o matemática. La respuesta suelo publicarla unas semanas después.
Problema 67
En una isla viven veraces y embusteros. Los veraces siempre dicen la verdad y los embusteros siempre mienten. Un día, un viajero se encuentra con dos isleños, y le pregunta al más alto:
- ¿Sois ambos veraces?
Como por su respuesta no saca nada, le pregunta al más bajo si su compañero es veraz o no, a lo que el bajo le responde. Con su respuesta, el viajero es capaz de saber quién es veraz y quién es embustero. ¿Podrías saberlo tú?
Problema 66
Sabiendo que el área de la porción inferior sombreada es de 38 cm2, calcula el área de todo el triángulo. Nota: la altura está dividida en 10 segmentos de igual longitud (h).
Problema 65 (mostar solución)
Demuestra la siguiente desigualdad para todo x, y perteneciente a los reales y para todo a, b mayores o iguales que 0 que cumplan que a + b = 1.
Problema 64 (mostar solución)
x, y, z son enteros positivos. Halla todos los valores posibles del producto xyz.
Problema 63 (mostar solución)
Demostrar que si z es raíz doble del polinomio P(x), z es raíz simple del polinomio R(x).
Problema 62
Resuelve el siguiente límite:
Problema 61 (mostar solución)
Demuestra esta desigualdad para tres números reales cualesquiera:
Problema 60 (mostar solución)
Alberto, Blanca y Carlos son músicos. El saxofonista hoy no puede tocar con el guitarrista (como es habitual) ya que el guitarrista está tocando con el pianista. El pianista gana al mes 1000 € más que el saxofonista. Carlos solo gana 750 € mensuales. Blanca y Carlos no se conocen. ¿Qué instrumento toca cada uno?
Problema 59 (mostar solución)
Al dividir P(x) por (x+2), (x-2) y (x+3), obtenemos como resto 4, 8 y 13 respectivamente. Determina el resto de dividir P(x) entre Q(x) = (x+2)(x-2)(x+3).
Problema 58 (mostar solución)
Calcula la suma de las áreas de los círculos azules, en función de r1 y d1, suponiendo que la sucesión se continua indefinidamente. Los círculos son tangentes a las dos semirrectas y a los círculos anterior y posterior.
Problema 57 (mostar solución)
Calcula el valor de la expresión:
Problema 56 (mostar solución)
Tenemos una función f(x) = ax + b. Se verifica que f(f(f(1))) = 29, y que f(f(f(0))) = 2. ¿Cuánto vale "a"?
Problema 55 (mostar solución)
Una crema de queso posee un 24% de materia grasa en total, pero en seco tiene un 64% de materia grasa. ¿Qué porcentaje de agua tiene dicho producto?
Problema 54 (mostar solución)
Demuestra la siguiente igualdad:
Problema 53 (mostar solución)
Dos amigos están bebiendo, respectivamente, café y té. El primero introduce una cucharada de café en la taza de té de su amigo, y después el segundo hace lo mismo echando una cucharada de té en la taza de café. ¿Habrá más café en la de té o más té en la de café? Suponemos que la capacidad de las cucharas es igual.
Problema 52 (mostar solución)
Demuestra que si a y b son dos reales positivos, se verifica la siguiente desigualdad.
Problema 51 (mostar solución)
Calcula el resultado de la siguiente operación:
Problema 50 (mostar solución)
Una ciudad tiene 8.000 habitantes. Parte de ellos se van de vacaciones en verano. De los que quedan, al 63,6363...% les gusta la música, mientras que al 22,297297...% les gusta vestir vaqueros. ¿Cuántos se fueron de vacaciones en verano?
Problema 49 (mostar solución)
Si a 32 le restamos 2, el resultado es múltiplo de 5. Si a 243 le restamos 3, el resultado también es múltimplo de 5. ¿Será siempre cierto que n^5 - n es siempre múltiplo de 5 para cualquier valor de n?
Problema 48 (mostar solución)
¿Cómo demostrarías que la raíz cuadrada de 2 es un número irracional?
Problema 47
Alicia conoció a dos animales: un león y un unicornio. El león mentía lunes, martes y miércoles, y decía la verdad los demás días, mientras que el unicornio mentía jueves, viernes y sábado, y decía la verdad los demás días.
Más tarde conoció a dos hermanos: Twedledum y Twedledee. Sabía que uno de ellos seguía las costumbres del león y el otro las del unicornio, en lo que a mentir y decir la verdad se refiere, pero no sabía quién seguía a quién.
Un día la niña salió a pasear y se encontró con los dos hermanos. Éstos le comentaron lo siguiente:
El primero: Hoy no es domingo.
El segundo: De hecho, hoy es lunes.
El primero: Mañana es uno de los días en los que le toca mentir a Twedledee.
El segundo: El león mintió ayer.
A partir de estos comentarios, intenta responder a las siguientes preguntas:
1.- ¿Qué día de la semana es?
2.- ¿Cuál es los dos es Twedledum?
3.- ¿Cuál de los dos sigue al león y cuál al unicornio?
Problema 46 (mostar solución)
Dos trenes se aproximan entre sí a una velocidad v. Cuando se encuentran a una distancia d, ambos comienzan a frenar con la misma aceleración justo para no chocarse pero quedar juntos. En ese momento, cuando empiezan ambos a decelerar, sale un pájaro desde uno de los trenes hasta el otro a una velocidad 2v. Cuando alcanza el otro tren, se da la vuelta y realiza el mismo proceso hasta que ambos trenes están juntos. ¿Cuántas veces recorre más el pájaro que la distancia d?
Problema 45 (mostar solución)
Averigua en cuántos ceros termina el número 100!
Problema 44 (mostar solución)
Demuestra que si en una fiesta el número de saludos es impar, el total de personas es par. Nota: solo se saludan una vez entre dos personas, uno no se saluda consigo mismo y al final de la fiesta cada persona se ha saludado con el resto.
Problema 43 (mostar solución)
Imagina que un satélite se encuentra siempre encima de una determinada población. Determina su altura y la relación entre su energía potencial y su energía cinética.
Problema 42 (mostar solución)
Alberto, Basilio y Carlos están condenados a muerte, pero debido a una serie de problemas legales solo ejecutarán a uno de los tres. Basilio es muy amigo del ejecutor, por lo que le pide que le diga cuál de sus amigos se va a salvar. El ejecutor le contesta que Alberto se va a salvar. ¿Quién tiene más probabilidades de morir, Basilio o Carlos?
Problema 41
Desde un rascacielos de 700 m lanzamos una pelota. Cuando bota en el suelo pierde 1/3 de su energía mecánica. ¿Cuánto tiempo tarda en dejar de botar? Considera nulo la fricción del aire.
¿Qué altura debería tener el edificio para que la pelota deje de botar en 1 minuto? ¿Cuánto aumenta el tiempo si duplicamos la altura de lanzamiento?
Problema 40 (mostar solución)
Determina el área del siguiente círculo:
Problema 39 (mostar solución)
Una isla está formada por 30 personas, todas ellas tienen los ojos azules. Si alguien sabe que tiene los ojos azules, debe suicidarse al amanecer del día siguiente, pero está prohibido hablar de los ojos de los demás ni mirarse los propios. Un soleado 21 de mayo, aparece un genio en la isla y dice: "al menos uno de vosotros tiene los ojos azules". Determina a partir de qué día estarán todos muertos.
Problema 38 (mostar solución)
Un explorador se encuentra en un punto de la Tierra. Un día, camina 5 km al sur, 5 km al este y 5 km al norte, regresando así al mismo punto. ¿Dónde se encuentra ese punto? Dato: el lugar más al norte que ha visitado ese hombre es Islandia.
Problema 37 (mostar solución)
Tenemos un vaso de 20 cm de altura hasta la mitad de agua, y le introducimos un cubito de hielo de masa 50g. Por consiguiente, el nivel del agua aumenta hasta las 3/4 partes del total del vaso. ¿Hasta que altura subirá el agua cuando se derrita todo el hielo?
Problema 36 (mostar solución)
Nos encontramos ante la puerta de una habitación cerrada, que solo podremos abrir una vez. A la puerta hay 3 interruptores, y solo uno de ellos enciende una bombilla de dentro. Determina una estrategia para averiguar cuál es. Recuerda que solo puedes entrar en la habitación una vez, y cuando entras, no puedes tocar más los interruptores.
Problema 35 (mostar solución)
Un ciclista va desde la ciudad A hasta la ciudad B. ¿A qué velocidad debe regresar a la ciudad A para que la velocidad media total sea el doble que la de la ida?
Problema 34 (mostar solución)
Un perro tiene atada una campana a su cola de tal modo que cuando corre, suena. Cuando el perro la oye, aumenta su velocidad de carrera en 1 m/s. Suponiendo que pudiese alcanzar cualquier velocidad, ¿Cuál sería esta?
Problema 33 (mostar solución)
Nos desplazamos en coche a una velocidad constante de 5 m/s. En un instante de tiempo t, lanzamos hacia delante en el sentido y dirección de la trayectoria del vehículo una pelota a 5 m/s. El coche continua a 5 m/s después del lanzamiento. Se nos ocurre la idea de calcular la energía cinética de esa pelota, y lo hacemos sumando a la energía que disponía antes del lanzamiento, la que le añadimos. Si llamamos m a la masa de esa pelota, su energía cinética dentro del coche será 1/2*m*25 Julios, y como la lanzamos a 5 m/s, le añadimos otros 1/2*m*25 Julios, por lo que la energía total de la pelota será de 25m Julios.
Un amigo fuera del coche decide medir la energía de esa pelota, pero de forma diferente. Él se basa en su velocidad final de 10 m/s, por lo que su energía cinética sería de 50m Julios.
¿Cómo es posible que la misma pelota tenga energías diferentes? ¿Dónde está el error? ¿Dónde está la energía "que falta"?
Problema 32 (mostar solución)
Problema 31 (mostar solución)
Tenemos dos recipientes idénticos de altura 10 cm con forma de cono, uno sobre el otro, como en la figura:
Problema 30 (mostar solución)
Las naves espaciales A y B se dirigen por el vacío hacia el planeta rojo a una velocidad de 50.000 km/s. El ángulo que forman sus trayectorias es de 60º, y la distancia que inicialmente las separa a ambas es de 3.000.000 km. En ese momento, la nave A envía una onda de radio a la nave B, que rebota entre ellas hasta que ambas llegan al planeta rojo. ¿Cuánta distancia recorre esa onda?
Problema 29 (mostar solución)
Mario camina a 5 km/h todas las mañanas desde su casa hasta el parque. Hay 1500 metros. Va acompañado de su perro que corre a 15 km/h. Cuando el perro llega al parque, se da la vuelta hacia donde está su dueño, y vuelve hacia el parque. Repite el mismo proceso hasta que Mario llega al parque. Después, ambos regresan juntos a una velocidad de 7 km/h a casa. ¿Cuántos km recorre el perro en su paseo matutino?
Problema 28 (mostar solución)
Tenemos un globo que duplica su volumen cada día. Introduciéndolo en una habitación, tarda 30 días en llenarla entera. ¿Cuántos días tardará en llenarse la habitación si inicialmente había dos globos iguales?
Problema 27 (mostar solución)
Un físico iba pensando en sus ecuaciones sobre la Teoría de Supercuerdas mientras conducía, como cualquier mañana normal. De repente, se da cuenta de que le perseguía la policía por saltarse un semáforo en rojo, pero como es físico, intenta pensar una escusa rápida e ingeniosa. Le dice al policía (que casualmente también sabe de física porque lee el blog Ciencia como nunca) que no vio el semáforo rojo, sino verde, debido al efecto Doppler. De todos modos, el agente le puso una multa por exceso de velocidad...¿A qué velocidad iba nuestro amigo el físico? (La longitud de onda del rojo es de 650 nm y la del verde es de 520 nm).
Nota: ayúdate de las ecuaciones de la entrada sobre el Efecto Doppler Relativista.
Problema 26 (mostar solución)
Un joven llega a un puente ferroviario y comienza a correr por él. Cuando ha recorrido 3/8 del puente, escucha que se acerca el tren. Pensó: "dada la velocidad que lleva el tren, voy a morir atropellado". ¿Qué velocidad mínima llevaba ese tren? Nota: para salvarse necesita escapar por uno de los dos extremos del puente. El joven corre a 10 km/h.
Problema 25 (mostar solución)
Sabiendo que en cada interrogante hay un número secreto y sabiendo que cada número negro se forma sumando todos los números secretos excepto el que está en ese mismo vértice, determina todos los números invisibles del polígono de la imagen inferior. Para ello, busca una fórmula general que te ayude a encontarlos para cualquier polígono de n lados.
Problema 24 (mostar solución)
Determina el valor de la siguiente expresión:
Problema 23 (mostar solución)
Calcula el valor de la siguiente suma:
Problema 22 (mostar solución)
Este problema se le atribuye a Albert Einstein, quien dijo que el 97% de la población mundial no podría resolverlo. ¿Podrás tú?
1.- Tenemos 5 casas cada una de un color diferente.
2.- En cada casa vive una persona de distinta nacionalidad.
3.- Los 5 propietarios toman bebidas diferentes, fuman distintas marcas y tienen distintas mascotas.
1.- El Ingles vive en la casa Roja.
2.- La mascota del Español es un Perro.
3.- El Francés bebe Té.
4.- La casa Gris es la inmediata a la izquierda de la casa Blanca.
5.- El propietario de la casa Gris toma Café.
6.- La persona que fuma Winston cría Pájaros.
7.- El propietario de la casa Amarilla fuma Camel.
8.- El hombre que vive en la casa del Centro toma Leche.
9.- El Italiano vive en la Primera casa.
10.-La persona que fuma Ducados vive junto a la que tiene Gatos.
11.-El hombre que tiene Caballos vive junto al que fuma Camel.
12.-La persona que fuma Blend bebe Cerveza.
13.-El Suizo fuma Habanos.
14.-El Italiano vive junto a la casa Azul.
15.-El hombre que fuma Ducados tiene un vecino que bebe Agua.
¿Quién tiene como mascotas a los Peces?
Problema 21 (mostar solución)
Un matemático posee una finca triangular. En su testamento pone que deben repartirse ese terreno entre sus seis hijos de forma que a cada hijo le toque una superficie igual a la de sus hermanos. El hermano mayor propone trazar las medianas, ya que las seis áreas que se formarán serán iguales. ¿Estará en lo cierto o pretende estafar a sus hermanos? Pista: el hermano mayor pretende quedarse con una de los dos terrenos más próximos al mayor ángulo del triángulo.
Problema 20 (mostrar solución)
Determina el área roja sabiendo que la cuerda tangente a la circunferencia interior mide 100 m.
Problema 19 (mostrar solución)
Demuestra que la siguiente expresión es siempre múltiplo de 6 si sustituímos n por un natural mayor que 1:
Problema 18 (mostar solución)
¿Qué probabilidad hay de que algunas personas en un grupo de n cumplan años el mismo día?
Problema 17
Tenemos tres papeletas de la siguiente manera. Una es azul por las dos caras, otra roja por las dos caras y la última es roja por un lado y azul por el otro. Cogemos con los ojos cerrados una papeleta y vemos que tiene una cara roja. ¿Qué probabilidad hay de que al darle la vuelta sea también roja?
Problema 16
Un concurso de televisión consiste en lo siguiente: hay tres puertas en el escenario, y detrás de una hay un coche. Detrás de las otras dos no hay nada. El objetivo del juego es, lógicamente, ganar el coche. Para ello, el concursante debe escoger al azar una de las tres puertas.
Un determinado concursante elige la puerta "1". El presentador abre la puerta "2" y muestra que detrás de ella no hay nada, por lo que el coche estará detrás de la "1" o de la "3". Al concursante se le da la opción de cambiar de puerta. ¿Qué harías tú?
Problema 15
En una fiesta, todos los invitados se saludan con la mano con todos. En total se cuentan 325 apretones de manos. ¿Cuántos invitados había? (He contado hasta 4 formas de resolverlo)
Problema 14
Determina las últimas tres cifras de 7 elevado a 2014.
Problema 13
Demuestra por deducción que el valor absoluto de la suma de un número más su inverso es siempre mayor o igual a dos.
Problema 12
¿Será cierto que la suma de tres cubos consecutivos es siempre múltiplo de 9?
Problema 11
Calcula la suma de todos los números presentes en la fina nº 100 y determina una fórmula general para hallar la suma de los números de una fila n.
Problema 10
¿El producto de cuatro enteros consecutivos es siempre una unidad inferior a un cuadrado perfecto?¿Por qué es así o por qué no lo es?
Problema 9
Demuestra que al dividir el cuadrado de cualquier número primo mayor a 3 entre 12, el resto es siempre 1.
Problema 8
Al multiplicar un cuadrado perfecto por el número natural anterior y dividir el resultado entre 12, ¿cuál será el resto de la división y por qué? Ej: (16*15)/12.
Problema 7
¿Cuál es la relación existente entre el área sombreada de rojo y la de verde?
Problema 6
Siendo a y b números positivos, deduce la siguiente desigualdad matemática e indica cuándo se alcanza la igualdad.
Problema 5 (mostar solución)
Problema 4
Juan y María salen a pasear todos los días. Ayer fueron desde la Plaza hasta el Parque. Juan corrió la mitad de la distancia y anduvo la otra mitad. María corrió la mitad del tiempo y anduvo la otra mitad. Suponiendo que ambos salieron a la vez, corren a la misma velocidad y andan a la misma velocidad, ¿quién llegó antes al Parque?
Problema 3
El de hoy es una demostración matemática. ¿Es cierta la siguiente igualdad? Generalízala.
Problema 67
En una isla viven veraces y embusteros. Los veraces siempre dicen la verdad y los embusteros siempre mienten. Un día, un viajero se encuentra con dos isleños, y le pregunta al más alto:
- ¿Sois ambos veraces?
Como por su respuesta no saca nada, le pregunta al más bajo si su compañero es veraz o no, a lo que el bajo le responde. Con su respuesta, el viajero es capaz de saber quién es veraz y quién es embustero. ¿Podrías saberlo tú?
Problema 66
Sabiendo que el área de la porción inferior sombreada es de 38 cm2, calcula el área de todo el triángulo. Nota: la altura está dividida en 10 segmentos de igual longitud (h).
Problema 65 (mostar solución)
Demuestra la siguiente desigualdad para todo x, y perteneciente a los reales y para todo a, b mayores o iguales que 0 que cumplan que a + b = 1.
Problema 64 (mostar solución)
x, y, z son enteros positivos. Halla todos los valores posibles del producto xyz.
Problema 63 (mostar solución)
Demostrar que si z es raíz doble del polinomio P(x), z es raíz simple del polinomio R(x).
Problema 62
Resuelve el siguiente límite:
Problema 61 (mostar solución)
Demuestra esta desigualdad para tres números reales cualesquiera:
Problema 60 (mostar solución)
Alberto, Blanca y Carlos son músicos. El saxofonista hoy no puede tocar con el guitarrista (como es habitual) ya que el guitarrista está tocando con el pianista. El pianista gana al mes 1000 € más que el saxofonista. Carlos solo gana 750 € mensuales. Blanca y Carlos no se conocen. ¿Qué instrumento toca cada uno?
Problema 59 (mostar solución)
Al dividir P(x) por (x+2), (x-2) y (x+3), obtenemos como resto 4, 8 y 13 respectivamente. Determina el resto de dividir P(x) entre Q(x) = (x+2)(x-2)(x+3).
Problema 58 (mostar solución)
Calcula la suma de las áreas de los círculos azules, en función de r1 y d1, suponiendo que la sucesión se continua indefinidamente. Los círculos son tangentes a las dos semirrectas y a los círculos anterior y posterior.
Problema 57 (mostar solución)
Calcula el valor de la expresión:
Problema 56 (mostar solución)
Tenemos una función f(x) = ax + b. Se verifica que f(f(f(1))) = 29, y que f(f(f(0))) = 2. ¿Cuánto vale "a"?
Problema 55 (mostar solución)
Una crema de queso posee un 24% de materia grasa en total, pero en seco tiene un 64% de materia grasa. ¿Qué porcentaje de agua tiene dicho producto?
Problema 54 (mostar solución)
Demuestra la siguiente igualdad:
Problema 53 (mostar solución)
Dos amigos están bebiendo, respectivamente, café y té. El primero introduce una cucharada de café en la taza de té de su amigo, y después el segundo hace lo mismo echando una cucharada de té en la taza de café. ¿Habrá más café en la de té o más té en la de café? Suponemos que la capacidad de las cucharas es igual.
Problema 52 (mostar solución)
Demuestra que si a y b son dos reales positivos, se verifica la siguiente desigualdad.
Problema 51 (mostar solución)
Calcula el resultado de la siguiente operación:
Problema 50 (mostar solución)
Una ciudad tiene 8.000 habitantes. Parte de ellos se van de vacaciones en verano. De los que quedan, al 63,6363...% les gusta la música, mientras que al 22,297297...% les gusta vestir vaqueros. ¿Cuántos se fueron de vacaciones en verano?
Problema 49 (mostar solución)
Si a 32 le restamos 2, el resultado es múltiplo de 5. Si a 243 le restamos 3, el resultado también es múltimplo de 5. ¿Será siempre cierto que n^5 - n es siempre múltiplo de 5 para cualquier valor de n?
Problema 48 (mostar solución)
¿Cómo demostrarías que la raíz cuadrada de 2 es un número irracional?
Problema 47
Alicia conoció a dos animales: un león y un unicornio. El león mentía lunes, martes y miércoles, y decía la verdad los demás días, mientras que el unicornio mentía jueves, viernes y sábado, y decía la verdad los demás días.
Más tarde conoció a dos hermanos: Twedledum y Twedledee. Sabía que uno de ellos seguía las costumbres del león y el otro las del unicornio, en lo que a mentir y decir la verdad se refiere, pero no sabía quién seguía a quién.
Un día la niña salió a pasear y se encontró con los dos hermanos. Éstos le comentaron lo siguiente:
El primero: Hoy no es domingo.
El segundo: De hecho, hoy es lunes.
El primero: Mañana es uno de los días en los que le toca mentir a Twedledee.
El segundo: El león mintió ayer.
A partir de estos comentarios, intenta responder a las siguientes preguntas:
1.- ¿Qué día de la semana es?
2.- ¿Cuál es los dos es Twedledum?
3.- ¿Cuál de los dos sigue al león y cuál al unicornio?
Problema 46 (mostar solución)
Dos trenes se aproximan entre sí a una velocidad v. Cuando se encuentran a una distancia d, ambos comienzan a frenar con la misma aceleración justo para no chocarse pero quedar juntos. En ese momento, cuando empiezan ambos a decelerar, sale un pájaro desde uno de los trenes hasta el otro a una velocidad 2v. Cuando alcanza el otro tren, se da la vuelta y realiza el mismo proceso hasta que ambos trenes están juntos. ¿Cuántas veces recorre más el pájaro que la distancia d?
Problema 45 (mostar solución)
Averigua en cuántos ceros termina el número 100!
Problema 44 (mostar solución)
Demuestra que si en una fiesta el número de saludos es impar, el total de personas es par. Nota: solo se saludan una vez entre dos personas, uno no se saluda consigo mismo y al final de la fiesta cada persona se ha saludado con el resto.
Problema 43 (mostar solución)
Imagina que un satélite se encuentra siempre encima de una determinada población. Determina su altura y la relación entre su energía potencial y su energía cinética.
Problema 42 (mostar solución)
Alberto, Basilio y Carlos están condenados a muerte, pero debido a una serie de problemas legales solo ejecutarán a uno de los tres. Basilio es muy amigo del ejecutor, por lo que le pide que le diga cuál de sus amigos se va a salvar. El ejecutor le contesta que Alberto se va a salvar. ¿Quién tiene más probabilidades de morir, Basilio o Carlos?
Problema 41
Desde un rascacielos de 700 m lanzamos una pelota. Cuando bota en el suelo pierde 1/3 de su energía mecánica. ¿Cuánto tiempo tarda en dejar de botar? Considera nulo la fricción del aire.
¿Qué altura debería tener el edificio para que la pelota deje de botar en 1 minuto? ¿Cuánto aumenta el tiempo si duplicamos la altura de lanzamiento?
Problema 40 (mostar solución)
Determina el área del siguiente círculo:
Problema 39 (mostar solución)
Una isla está formada por 30 personas, todas ellas tienen los ojos azules. Si alguien sabe que tiene los ojos azules, debe suicidarse al amanecer del día siguiente, pero está prohibido hablar de los ojos de los demás ni mirarse los propios. Un soleado 21 de mayo, aparece un genio en la isla y dice: "al menos uno de vosotros tiene los ojos azules". Determina a partir de qué día estarán todos muertos.
Problema 38 (mostar solución)
Un explorador se encuentra en un punto de la Tierra. Un día, camina 5 km al sur, 5 km al este y 5 km al norte, regresando así al mismo punto. ¿Dónde se encuentra ese punto? Dato: el lugar más al norte que ha visitado ese hombre es Islandia.
Problema 37 (mostar solución)
Tenemos un vaso de 20 cm de altura hasta la mitad de agua, y le introducimos un cubito de hielo de masa 50g. Por consiguiente, el nivel del agua aumenta hasta las 3/4 partes del total del vaso. ¿Hasta que altura subirá el agua cuando se derrita todo el hielo?
Problema 36 (mostar solución)
Nos encontramos ante la puerta de una habitación cerrada, que solo podremos abrir una vez. A la puerta hay 3 interruptores, y solo uno de ellos enciende una bombilla de dentro. Determina una estrategia para averiguar cuál es. Recuerda que solo puedes entrar en la habitación una vez, y cuando entras, no puedes tocar más los interruptores.
Problema 35 (mostar solución)
Un ciclista va desde la ciudad A hasta la ciudad B. ¿A qué velocidad debe regresar a la ciudad A para que la velocidad media total sea el doble que la de la ida?
Problema 34 (mostar solución)
Un perro tiene atada una campana a su cola de tal modo que cuando corre, suena. Cuando el perro la oye, aumenta su velocidad de carrera en 1 m/s. Suponiendo que pudiese alcanzar cualquier velocidad, ¿Cuál sería esta?
Problema 33 (mostar solución)
Nos desplazamos en coche a una velocidad constante de 5 m/s. En un instante de tiempo t, lanzamos hacia delante en el sentido y dirección de la trayectoria del vehículo una pelota a 5 m/s. El coche continua a 5 m/s después del lanzamiento. Se nos ocurre la idea de calcular la energía cinética de esa pelota, y lo hacemos sumando a la energía que disponía antes del lanzamiento, la que le añadimos. Si llamamos m a la masa de esa pelota, su energía cinética dentro del coche será 1/2*m*25 Julios, y como la lanzamos a 5 m/s, le añadimos otros 1/2*m*25 Julios, por lo que la energía total de la pelota será de 25m Julios.
Un amigo fuera del coche decide medir la energía de esa pelota, pero de forma diferente. Él se basa en su velocidad final de 10 m/s, por lo que su energía cinética sería de 50m Julios.
¿Cómo es posible que la misma pelota tenga energías diferentes? ¿Dónde está el error? ¿Dónde está la energía "que falta"?
Problema 32 (mostar solución)
Problema 31 (mostar solución)
Tenemos dos recipientes idénticos de altura 10 cm con forma de cono, uno sobre el otro, como en la figura:
El cono de arriba está lleno de agua, que gotea poco a poco hacia el de abajo. Se pide calcular la altura del agua en el cono de abajo cuando el cono de arriba se ha vaciado hasta una altura de 5 cm.
Problema 30 (mostar solución)
Las naves espaciales A y B se dirigen por el vacío hacia el planeta rojo a una velocidad de 50.000 km/s. El ángulo que forman sus trayectorias es de 60º, y la distancia que inicialmente las separa a ambas es de 3.000.000 km. En ese momento, la nave A envía una onda de radio a la nave B, que rebota entre ellas hasta que ambas llegan al planeta rojo. ¿Cuánta distancia recorre esa onda?
Problema 29 (mostar solución)
Mario camina a 5 km/h todas las mañanas desde su casa hasta el parque. Hay 1500 metros. Va acompañado de su perro que corre a 15 km/h. Cuando el perro llega al parque, se da la vuelta hacia donde está su dueño, y vuelve hacia el parque. Repite el mismo proceso hasta que Mario llega al parque. Después, ambos regresan juntos a una velocidad de 7 km/h a casa. ¿Cuántos km recorre el perro en su paseo matutino?
Problema 28 (mostar solución)
Tenemos un globo que duplica su volumen cada día. Introduciéndolo en una habitación, tarda 30 días en llenarla entera. ¿Cuántos días tardará en llenarse la habitación si inicialmente había dos globos iguales?
Problema 27 (mostar solución)
Un físico iba pensando en sus ecuaciones sobre la Teoría de Supercuerdas mientras conducía, como cualquier mañana normal. De repente, se da cuenta de que le perseguía la policía por saltarse un semáforo en rojo, pero como es físico, intenta pensar una escusa rápida e ingeniosa. Le dice al policía (que casualmente también sabe de física porque lee el blog Ciencia como nunca) que no vio el semáforo rojo, sino verde, debido al efecto Doppler. De todos modos, el agente le puso una multa por exceso de velocidad...¿A qué velocidad iba nuestro amigo el físico? (La longitud de onda del rojo es de 650 nm y la del verde es de 520 nm).
Nota: ayúdate de las ecuaciones de la entrada sobre el Efecto Doppler Relativista.
Problema 26 (mostar solución)
Un joven llega a un puente ferroviario y comienza a correr por él. Cuando ha recorrido 3/8 del puente, escucha que se acerca el tren. Pensó: "dada la velocidad que lleva el tren, voy a morir atropellado". ¿Qué velocidad mínima llevaba ese tren? Nota: para salvarse necesita escapar por uno de los dos extremos del puente. El joven corre a 10 km/h.
Problema 25 (mostar solución)
Problema 24 (mostar solución)
Determina el valor de la siguiente expresión:
Problema 23 (mostar solución)
Calcula el valor de la siguiente suma:
Problema 22 (mostar solución)
Este problema se le atribuye a Albert Einstein, quien dijo que el 97% de la población mundial no podría resolverlo. ¿Podrás tú?
1.- Tenemos 5 casas cada una de un color diferente.
2.- En cada casa vive una persona de distinta nacionalidad.
3.- Los 5 propietarios toman bebidas diferentes, fuman distintas marcas y tienen distintas mascotas.
1.- El Ingles vive en la casa Roja.
2.- La mascota del Español es un Perro.
3.- El Francés bebe Té.
4.- La casa Gris es la inmediata a la izquierda de la casa Blanca.
5.- El propietario de la casa Gris toma Café.
6.- La persona que fuma Winston cría Pájaros.
7.- El propietario de la casa Amarilla fuma Camel.
8.- El hombre que vive en la casa del Centro toma Leche.
9.- El Italiano vive en la Primera casa.
10.-La persona que fuma Ducados vive junto a la que tiene Gatos.
11.-El hombre que tiene Caballos vive junto al que fuma Camel.
12.-La persona que fuma Blend bebe Cerveza.
13.-El Suizo fuma Habanos.
14.-El Italiano vive junto a la casa Azul.
15.-El hombre que fuma Ducados tiene un vecino que bebe Agua.
¿Quién tiene como mascotas a los Peces?
Problema 21 (mostar solución)
Un matemático posee una finca triangular. En su testamento pone que deben repartirse ese terreno entre sus seis hijos de forma que a cada hijo le toque una superficie igual a la de sus hermanos. El hermano mayor propone trazar las medianas, ya que las seis áreas que se formarán serán iguales. ¿Estará en lo cierto o pretende estafar a sus hermanos? Pista: el hermano mayor pretende quedarse con una de los dos terrenos más próximos al mayor ángulo del triángulo.
Problema 20 (mostrar solución)
Determina el área roja sabiendo que la cuerda tangente a la circunferencia interior mide 100 m.
Problema 19 (mostrar solución)
Demuestra que la siguiente expresión es siempre múltiplo de 6 si sustituímos n por un natural mayor que 1:
Problema 18 (mostar solución)
¿Qué probabilidad hay de que algunas personas en un grupo de n cumplan años el mismo día?
Problema 17
Tenemos tres papeletas de la siguiente manera. Una es azul por las dos caras, otra roja por las dos caras y la última es roja por un lado y azul por el otro. Cogemos con los ojos cerrados una papeleta y vemos que tiene una cara roja. ¿Qué probabilidad hay de que al darle la vuelta sea también roja?
Problema 16
Un concurso de televisión consiste en lo siguiente: hay tres puertas en el escenario, y detrás de una hay un coche. Detrás de las otras dos no hay nada. El objetivo del juego es, lógicamente, ganar el coche. Para ello, el concursante debe escoger al azar una de las tres puertas.
Un determinado concursante elige la puerta "1". El presentador abre la puerta "2" y muestra que detrás de ella no hay nada, por lo que el coche estará detrás de la "1" o de la "3". Al concursante se le da la opción de cambiar de puerta. ¿Qué harías tú?
Problema 15
En una fiesta, todos los invitados se saludan con la mano con todos. En total se cuentan 325 apretones de manos. ¿Cuántos invitados había? (He contado hasta 4 formas de resolverlo)
Problema 14
Determina las últimas tres cifras de 7 elevado a 2014.
Problema 13
Demuestra por deducción que el valor absoluto de la suma de un número más su inverso es siempre mayor o igual a dos.
Problema 12
¿Será cierto que la suma de tres cubos consecutivos es siempre múltiplo de 9?
Problema 11
Calcula la suma de todos los números presentes en la fina nº 100 y determina una fórmula general para hallar la suma de los números de una fila n.
Problema 10
¿El producto de cuatro enteros consecutivos es siempre una unidad inferior a un cuadrado perfecto?¿Por qué es así o por qué no lo es?
Problema 9
Demuestra que al dividir el cuadrado de cualquier número primo mayor a 3 entre 12, el resto es siempre 1.
Problema 8
Al multiplicar un cuadrado perfecto por el número natural anterior y dividir el resultado entre 12, ¿cuál será el resto de la división y por qué? Ej: (16*15)/12.
Problema 7
¿Cuál es la relación existente entre el área sombreada de rojo y la de verde?
Problema 6
Siendo a y b números positivos, deduce la siguiente desigualdad matemática e indica cuándo se alcanza la igualdad.
Problema 5 (mostar solución)
Problema 4
Juan y María salen a pasear todos los días. Ayer fueron desde la Plaza hasta el Parque. Juan corrió la mitad de la distancia y anduvo la otra mitad. María corrió la mitad del tiempo y anduvo la otra mitad. Suponiendo que ambos salieron a la vez, corren a la misma velocidad y andan a la misma velocidad, ¿quién llegó antes al Parque?
Problema 3
El de hoy es una demostración matemática. ¿Es cierta la siguiente igualdad? Generalízala.
Problema 2
En el mundo mágico de animales fantásticos conviven el Dinosaurio y el Pegaso. El Dinosaurio miente los lunes, martes y miércoles, mientras que el Pegaso lo hace los jueves, viernes y sábados. En todas las demás ocasiones ambos dicen la verdad. El otro día, abmos mantuvieron esta conversación:
-Ayer me tocó mentir- dijo el Dinosaurio.
-También a mí me tocó mentir- contestó el Pegaso.
¿En qué día se encontraron?
Problema 1
En el mundo mágico de animales fantásticos conviven el Dinosaurio y el Pegaso. El Dinosaurio miente los lunes, martes y miércoles, mientras que el Pegaso lo hace los jueves, viernes y sábados. En todas las demás ocasiones ambos dicen la verdad. El otro día, abmos mantuvieron esta conversación:
-Ayer me tocó mentir- dijo el Dinosaurio.
-También a mí me tocó mentir- contestó el Pegaso.
¿En qué día se encontraron?
Problema 1
Lanzamos una flecha desde el suelo con ayuda de un muelle de constante elástica K=500N/m, comprimiéndolo 10 cm. La flecha tiene una masa de 50g y se dirige hacia una manzana que está a 2m sobre el suelo.
Se pide calcular el ángulo de lanzamiento y la distancia horizontal (d) a la que debe lanzarse la flecha sabiendo que ésta se clava en la manzana de forma perfectamente horizontal.
Y si os atrevéis...calculad la masa de la manzana (m) sabiendo que el conjunto flecha-manzana cae a 6,25 m del punto de lanzamiento.



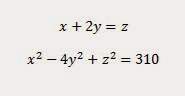














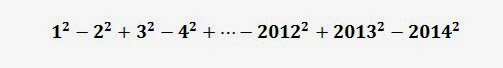







jueves
ResponderEliminar133 gramos la manzana y un ángulo de 38,75º
ResponderEliminarSiempre va a tardar menos Maria, la única forma de que no fuera asi seria que la diferencia entre la velocidad cuando corres y cuando andas tendiera a 0, pero entonces tardarían lo mismo. La diferencia pues de tiempos depende directamente de la diferencia de velocidades correr-andar e inversamente de la velocidad de correr de ambos.
ResponderEliminarEn el ultimo, el producto desde n hasta n+3, sumándole uno ed el cuadrado de (n*(n+1))+(2n+1), y el de las áreas son iguales
ResponderEliminarNo estoy de acuerdo con tu solucióndel problema 35, al menos mno al 100%.Imaginemos que su antiyo viaja en dirección contraria, al llegar a la mitad del camino se aniquilaran y algún fotón saldrá en dirección opesta al ciclista, ese fotón tardaría 0 s en recorrer la distancia en xuestio y habría doblado su v inicial.
ResponderEliminarEn caso de que su antiyó no se aniquilase debido a la materia de nuestro planeta, la colisión de ambos producirá fotones en todas las direcciones del espacio. ¿Cuánto tarda el fotón en llegar desde una ciudad a otra? t = d/c, es decir, el tiempo es igual a la distancia entre la velocidad de ese fotón (aunque en la atmósfera no sea c, nos sirve..).
EliminarPor lo tanto ese tiempo nunca será 0 y nunca conseguirá que su velocidad media sea el doble que la de ida. Nada puede superar c, por lo que nada tardará 0 s en ir de A a B o viceversa.
Saludos!
Tu respuesta es valida desde la perspectiva externa al fotón. Ese t habrías de multiplicarlo por beta para conocer el tiempo medido por el fotón. Recuerda que el tiempo y elespacio no son absolutos
EliminarPara el fotón, no hay distancia entre A y B, pero te recuerdo que la velocidad media del ciclista se tiene que calcular con el ciclista, no con los fotones que emitiría al chocar contra su antiyó. No tiene mucho sentido tu idea.
EliminarDesde la perspectiva del ciclista es imposible, y para el fotón también porque c es constante...
Creo que el que respondas lo del ciclista demuestra tu incapacidad para rebatirlo, si no, por que tratar de rebatirlo antes y ahora apelar a la imposibilidad del ejemplo?
ResponderEliminarPrimero: no es complicado rebatir algo que no tiene sentido lógico, físico y matemático. Tu ejemplo no es un buen ejemplo para decir que mi respuesta es incorrecta, y tus argumentos relativistas, menos todavía.
EliminarSegundo: esto es un blog de divulgación científica, no un lugar para que anónimos como tú falten al respeto a la gente.
Gabri, dejame a mi, su propuesta falla en que la velocidad, y por tanto el espacio y el tiempo, solo existen para cuerpos que se mueven a una v distinta de c, por tanto el fotón no entiende de velocidad y tu segunda parte no tiene sentido
ResponderEliminarEste comentario ha sido eliminado por un administrador del blog.
ResponderEliminar¡¡Excelentes problemas!!! MUY BUENOS PARA RECREARSE Y "AFLOJAR LAS TRIPAS DEL COCO"
ResponderEliminarLOS PROBLEMAS DE GEOMETRÍA,ME RECUERDAD LOS QUE DADO EN MI FUNCIÓN DE MAESTRO DE 7mo GRADO.RESUMEN.¡¡¡EXCELENTÍSIMOS!!!
ResponderEliminar