Cinemática y Gravitación

¿De qué depende el tiempo que tarda en caer un objeto en caída libre?

Como es lógico, de la altura. ¿Pero y la aceleración? ¿Es constante siempre? La respuesta es que no.

Esa aceleración se debe una fuerza de carácter gravitatorio, que a su vez depende de la distancia entre los cuerpos y sus masas (Ley de la Gravitación Universal). Como la fuerza aumenta conforme al objeto se acerque a la Tierra, también lo hará la aceleración para una masa m constante. Por esto, he decidido combinar las ecuaciones de cinemática con las de gravitación, para obtener unas nuevas que relacionen el tiempo de caída con la altura (teniendo en cuenta una aceleración variable). 

Esto quiere decir que la aceleración que sufre nuestro objeto depende de la altura, y nuestro objetivo será hallar la aceleración media entre el momento en el que está arriba del todo y el momento en el que toca el suelo. Recordemos las constantes con las que vamos a trabajar:

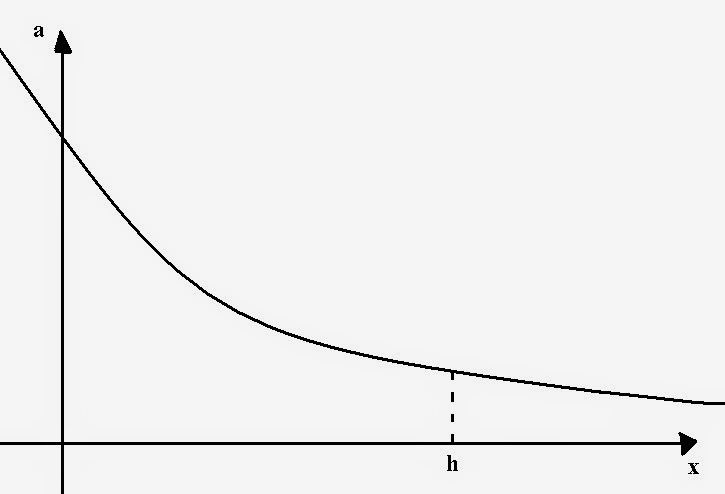
Si graficamos la aceleración en función de la altura, obtenemos una gráfica del siguiente tipo: (función potencial de exponente entero negativo par)

Cuando la altura vale 0, se obtiene el conocido valor de 9,8 m/s2 para la aceleración. A medida que la altura aumenta, este valor tiende a 0 en el infinito. Podemos observar que debajo de la función se forma un área:

Este área (A) corresponde geométricamente con la integral definida en el intervalo [0, h] de la función aceleración. Recordemos que la aceleración es la derivada de la velocidad con respecto al tiempo, entonces la integral indefinida de la función aceleración (diferencial de tiempo) corresponde con la función velocidad, que depende del tiempo con una aceleración constante. Podemos decir entonces que el área A se corresponde con la aceleración multiplicada por el tiempo. Podemos hallar la aceleración media así:

Esta nueva función tiene aceleración constante, y el área (A) de debajo en el intervalo [0, h] es la misma. Por eso podemos decir que la aceleración media se corresponde con ese área dividida entre h. Viéndolo como si fuese un rectángulo, el área A sería igual a la base h por la altura am.

Vamos a comparar las ecuaciones obtenidas con las ecuaciones "normales" donde consideramos la aceleración, g, constante:

Graficando las dos ecuaciones del tiempo con respecto a la altura obtenemos lo siguiente:

La altura (h) está representada en el eje de abscisas en km, y el tiempo (t) está representado en el eje de ordenadas en segundos. La línea negra es la fórmula con aceleración constante, y la línea roja es la que hemos hallado, donde la aceleración es variable.

Podemos observar que a alturas "pequeñas" las dos funciones están casi superpuestas. A partir de 300 o 400 km ya se observan diferencias que se van acrecentando con el tiempo. Para que nos hagamos una idea, la altura desde donde se lanzó Felix Baumgartner está representada por la línea azul, es decir, la diferencia de tiempos no alcanzaba ni 1 segundo.

Si representamos la altura de un objeto en función del tiempo que tarda en caer según las dos fórmulas:

De nuevo, la línea roja será la que hemos hallado en esta entrada y la negra la que considera la aceleración constante. A alturas bajas, hasta los 300 km, la diferencia es insignificante. A partir de esa altura, es un factor a tener en cuenta. Una altura de 200 km representa tan solo el 3% del radio terrestre.

Finalizaré la entrada recordando las dos ecuaciones que hemos hallado hoy, la que relaciona la altura (h) con respecto al tiempo y la que relaciona el tiempo (t) con respecto a la altura desde la que se lanza un cuerpo en caída libre:

Nota: considero todos los tiempos, lógicamente, como positivos si no pongo el símbolo "+" delante de las raíces.

Estas ecuaciones se pueden aplicar en otros planetas, sustituyeno el radio y la masa por el que corresponda. Es necesario decir también que en estas ecuaciones omitimos por completo el rozamiento con el aire, que es un factor muy a tener en cuenta. Los tiempos que hallemos con estas fórmulas serán ligeramente superiores a los experimentales por este motivo. Posteriormente ampliaré las ecuaciones teniendo en cuenta esos datos.

Hasta dentro de unos días con otra entrada. Espero que os haya gustado esta, ya que le he dedicado bastante tiempo entre obtener las ecuaciones y preparar la entrada y las gráficas.

Un saludo!