Zenón de Elea fue un filósofo griego muy conocido por plantear numerosas paradojas relacionadas con el movimiento. De entre todas ellas, la más famosa puede que sea la de Aquiles y la tortuga.
Aquiles decide echar una carrera a una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.
Todos sabemos que Aquiles ganará de sobra la carrera, igual que pensaba Zenón. Zenón planteó 40 paradojas de este estilo, debatiendo sobre el espacio, el tiempo y el movimiento. Proponía estos ejercicios mentales para reducir al absurdo las teorías de que la suma de infinitos números tenga que dar infinito.
Si la suma de infinitos sumandos siempre fuese igual a infinito, Aquiles nunca ganará la carrera, pero esto matemáticamente y físicamente no es así.
Supongamos que la velocidad de la tortuga es de 1 m/s, la velocidad de Aquiles es de 10 m/s y la ventaja inicial es de 100 m. En solo 10 segundos, Aquiles habrá alcanzado el punto desde el que sale la tortuga, y esta habrá avanzado 10 metros más. Esos 10 metros los recorre Aquiles en 1 segundo, pero la tortuga habrá avanzado 0,1 metros más...y así sucesivamente. Lo que plantea la paradoja es que 10 + 1 + 0,1 + ... da como resultado infinito, pero eso es incorrecto.
Cada vez, Aquiles tarda 10 veces menos en recorrer el trozo que lo separa de la tortuga. Esta fórmula nos puede ayudar a conocer todos los tiempos empleados (progresión geométrica decreciente):
 |
| Sucesión de tiempos empleados expresada en segundos |
Aplicando una fórmula que no vamos a demostrar ahora (fórmula de la suma de los infinitos términos de una progresión geométrica decreciente), podemos hallar la suma de esos tiempos. La demostración se realizaría restando a la suma de todos los términos, la suma multiplicada por la razón, pero por comodidad no lo vamos a hacer.
Como vemos en la imagen superior, la suma de 10 + 1 + 0,1...da como resultado 11,1 segundos. Aunque haya infinitos sumandos, el resultado es finito. Esto demuestra que Aquiles alcanza a la tortuga y lógicamente gana la carrera.
Podemos resolverlo también utilizando las leyes del movimiento, ya que conocemos las velocidades de ambos corredores la diferencia de posiciones. Igualando las posiciones conseguimos despejar el tiempo transcurrido en cruzarse.
Por lo tanto, una suma de infinitos términos decrecientes puede dar un resultado finito, como en este caso.
Podemos resolverlo también utilizando las leyes del movimiento, ya que conocemos las velocidades de ambos corredores la diferencia de posiciones. Igualando las posiciones conseguimos despejar el tiempo transcurrido en cruzarse.
Por lo tanto, una suma de infinitos términos decrecientes puede dar un resultado finito, como en este caso.
Un saludo, nos vemos en la próxima. No os olvidéis de compartir esta entrada!


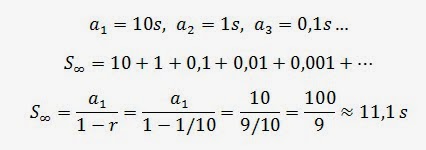

Hace diez años resolví la paradoja de Alquiles y la tortuga.la solución es muy sencilla, solo vasta usar simples herramientas del calculo que no se habían concebido para la época en que fue planteada, pero hoy en ha comienzo del siglo xxi, son el pan de cada día del estudiante de bachillerato.basta decir que en la solución no es ni siquiera necesario tener en cuenta el tiempo, ya que este y el espacio son una misma cosa. Sin embargo es muy interesante como se aborda en este articulo Jonny R Gonzalez.
ResponderEliminarBasta*
EliminarHace diez años resolví la paradoja de Alquiles y la tortuga.la solución es muy sencilla, solo vasta usar simples herramientas del calculo que no se habían concebido para la época en que fue planteada, pero hoy en ha comienzo del siglo xxi, son el pan de cada día del estudiante de bachillerato.basta decir que en la solución no es ni siquiera necesario tener en cuenta el tiempo, ya que este y el espacio son una misma cosa. Sin embargo es muy interesante como se aborda en este articulo Jonny R Gonzalez.
ResponderEliminarLa verdad
ResponderEliminarLa pregunta aquí sería, que si se diera la circunstancia de que Aquiles está por ejempli, cada minuto, 1/2 más cerca de la tortuga: si les separan 100m al siguiente minuto son 50m al siguiente 25m... (Teniendo en cuenta de que la velocidad que llevan es variable y no estable para que tenga sentido) ¿por qué nunca llegaría a alcanzarla? Si cada vez reduce la distancia a la mitad es porque por lento que vaya siempre va más rápido que la tortuga, entonces porque no llega al mismo punto que ella?
ResponderEliminarMuy buena repuesta
ResponderEliminarsi
ResponderEliminarAguante Aquiles
ResponderEliminar