El Teorema de la bola de pelo (Hairy ball theorem)

Cuando en el instituto (y en gran parte de la Universidad) hemos trabajado con vectores, siempre nos hemos limitado en su estudio a $\mathbb{R}^n$ como espacio vectorial. Fijémonos en el caso bidimensional para afianzar conceptos. Dotando a $\mathbb{R}^2$ de una estructura de espacio vectorial sobre el cuerpo de los números reales (mediante una operación de suma y otra de producto adecuadas), podemos tomar la base canónica en el plano con la cual podemos construir cualquier otro vector:

 

$\mathbb{R}^2$ como espacio vectorial siempre admite una base: todo vector de $\mathbb{R}^2$ puede escribirse como combinación lineal única de los elementos de la base. Por ejemplo, el vector $v$ (en verde) puede escribirse como $4e_x + 3 e_y$.

Podemos incluso ir más allá y no sólo considerar vectores en un punto, si no vectores en todos los puntos, es decir, campos vectoriales. En el caso plano sigue resultando cierto que existe una base global de campos vectoriales, y que por tanto todo campo vectorial puede escribirse como combinación lineal única de dichos vectores. Los coeficientes de la descomposición (en vulgo, las coordenadas) ya no son números reales, si no que son números reales punto a punto, es decir, funciones. Más adelante profundizaremos en las implicaciones que tiene esto.

En este caso, el campo vectorial $v$ define un vector en cada punto del plano. La base de campos vectoriales $e_x$ y $e_y$ está bien definida globalmente. La descomposición de $v$ en la base es única punto a punto. Es importante no confundir $\mathbb{R}^2$ como variedad con su espacio tangente, aunque sea algo a lo que estemos acostumbrados. Existe un isomorfismo entre ambos.

Pero el plano es un caso muy particular, poco interesante y una imagen nada realista de las superficies cotidianas que nos rodean. Es interesante, por tanto, estudiar otras variedades no planas, tales como esferas, toros y demás. No vamos a entrar en profundidad en las propiedades topológicas y geométricas de estos entes, pero daremos por supuesto que el plano y la (superficie de la) esfera no son en absoluto parecidos. Sin embargo, un huevo y una esfera se parecen un poco más. Matemáticamente esta relación se puede entender con ayuda de los isomorfismos topológicos (también llamados homeomorfismos). Diremos que dos espacios topológicos son homeomorfos, que a ojos de la topología viene a decir que son casi el mismo, si existe una biyección continua y con inversa continua entre ambos espacios. Entre una esfera y un huevo tal aplicación existe, pues podemos deformar uno en el otro (y viceversa) de forma continua. Entre el plano y la esfera no. Como digo, la topología sólo es capaz de distinguir las clases de equivalencia bajo homeomorfismos.

Un doctor en topología, cuando desayuna, tiene problemas como éste. A ojos de la topología, la taza y el dónut son equivalentes, pues existe un homeomorfismo entre ambos espacios topológicos.

Como digo, no entraremos en materia avanzada sobre geometría diferencial, pero hay una idea que tiene que quedar clara: sobre la esfera, o cualquier otra variedad no necesariamente bidimensional, también podemos construir vectores y campos de vectores. La idea es que punto a punto podemos construir un espacio vectorial denominado espacio tangente. 

Podemos visualizar el espacio tangente a la esfera en el punto $p$ vista desde $R^3$. Dicho espacio puede dotarse de una estructura de espacio vectorial, de modo que podemos construir vectores punto a punto sobre la esfera.

De igual modo a lo que hicimos en el plano, podemos tratar de construir campos vectoriales sobre la esfera. Formalmente, los campos vectoriales son secciones del fibrado tangente de la variedad. Pero sin entrar de momento en mucho detalle, los podemos imaginar visualmente.

El campo vectorial (en rojo) define un vector en cada punto de la esfera. Dicho vector vive en el espacio tangente a la esfera en dicho punto.

Pero ahora surge una diferencia radical con respecto al caso plano. En la esfera no podemos encontrar una base global de campos vectoriales. Dicho de otro modo, es imposible encontrar un campo vectorial sobre la esfera que no se anule en algún punto sobre la misma. Este resultado se conoce como el Teorema de la bola de pelo (Hairy ball theorem en inglés) y fue demostrado por Poincaré en 1885 para la 2-esfera. Más tarde se generalizó para dimensión arbitraria. Podéis encontrar una demostración al teorema en el siguiente enlace. En ella se asume la existencia de un campo vectorial sobre $S^2$ que no se anula en ningún punto y se llega a una contradicción. Emplea los conceptos de homotopía de curvas y de índice (winding number).

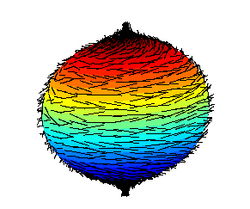Como se observa, este campo de vectores se anula en los polos, motivo por el que se conoce este resultado como que "no es posible peinar una esfera".

Sin embargo, existen otras variedades no planas que sí se pueden peinar, como es el caso del toro. Cuando una variedad admita una base global de campos vectoriales, diremos que dicha variedad es paralelizable. Como veremos, cuando esto ocurre, el fibrado tangente es trivial.

Este campo de vectores sobre el toro no se anula en ningún punto. Existe por tanto una base global de campos vectoriales sobre el toro.

¿Qué está sucediendo aquí? ¿Por qué hay variedades que se pueden peinar y otras que no? Dicho de otro modo: ¿por qué hay variedades sobre las que existe una base global de campos vectoriales y otras sobre las que no? Para responder a estas preguntas necesitamos estudiar lo que es un espacio vectorial sobre un cuerpo y lo que es un módulo sobre un anillo.

Un poco de álgebra

Comencemos por la estructura más general con las que vamos a trabajar: el anillo. Un anillo $(R,+,\cdot)$ es un sistema algebraico formado por un conjunto $R$ (del inglés ring) y dos operaciones cerradas, generalmente llamadas suma ($+$) y producto ($\cdot$), que cumplen las siguientes propiedades para cualesquiera $a,b,c\in R$:

(C) Conmutatividad para la suma: $a+b=b+a$.

(A) Asociatividad para la suma: $a+(b+c)=(a+b)+c$.

(N) Elemento neutro para la suma: $\exists 0\in R: 0+a=a$.

(I) Elemento inverso para la suma: $\exists (-a)\in R: a+(-a) = 0$.

Por tanto, $(R,+)$ tiene estructura de grupo abeliano. Para el producto:

(A) Asociatividad para el producto: $a\cdot b= b\cdot a$.

(D) Propiedad distributiva suma/producto: $a\cdot (b+c) = a\cdot b+a\cdot c$.

Si el anillo cuenta con un elemento neutro para el producto (N), que denotaremos mediante el símbolo $1\in R$, diremos que el anillo es unitario. Esto quiere decir que $\exists 1\in R:1\cdot a = a$. Si la operación de producto es conmutativa (C), es decir que $a\cdot b = b\cdot a$, se dice que el anillo es conmutativo. Finalmente, un anillo de división es un anillo unitario en el que todo elemento distinto de $0\in R$ posee un elemento inverso para el producto (I), es decir, $\forall a\neq 0 \exists a^{-1}\in R: a\cdot a^{-1} = 1$.

Para no perdernos en definiciones demasiado abstractas veamos un ejemplo concreto. Y es que un anillo es una estructura bastante natural en nuestro día a día. Por ejemplo, el conjunto de los enteros con las operaciones usuales de suma y de producto es un anillo conmutativo unitario. En efecto, la única propiedad que falla es la existencia de elemento inverso para el producto, ya que por ejemplo, el número 2, no tiene inverso en $\mathbb{Z}$. Para lo que sigue, es interesante comentar que el conjunto de funciones $C^{\infty}$ sobre la variedad $M$, que denotaremos por $C^{\infty}(M)$, es un anillo, pues existen funciones no nulas sobre la variedad que sí que pueden anularse en algunos puntos. En dichos puntos, por tanto, no está definida la función inversa (para el producto).

La siguiente estructura que necesitamos definir es la de cuerpo. Para ello podemos emplear la anterior definición de anillo, pues un cuerpo no es más que un anillo de división conmutativo, satisfaciendo las propiedades CANI (para la suma) y CANI D (para el producto). El conjunto de los reales con las operaciones usuales de suma y producto tiene estructura de cuerpo. En este caso, el número 2 sí que tiene inverso en $\mathbb{R}$, el 1/2.

Resumen de las propiedades de los anillos y del cuerpo.

A partir de un anillo y de un cuerpo se pueden definir unas nuevas estructuras denominadas módulo y espacio vectorial, respectivamente. Comencemos esta vez por el segundo, el espacio vectorial. 

Sea $K$ un cuerpo (del alemán, körper). Un $K$-espacio vectorial $(V,+,\cdot)$ es un conjunto $V$ equipado con unas operaciones cerradas de suma y de producto (no confundir con las del cuerpo) que satisfacen las siguientes propiedades para todos $a,b,c\in V$ y para todos $\alpha,\beta\in K$:

(C) Conmutatividad para la suma de vectores: $a+b=b+a$.

(A) Asociatividad de la suma: $(a+b)+c=a+(b+c)$.

(N) Elemento neutro en la suma: $\exists 0\in V: 0+a = a$.

(I) Elemento inverso para la suma: $\exists (-a)\in V: a+(-a)=0$.

(A) Asociatividad para el producto: $\alpha\cdot (\beta\cdot a) = (\alpha\cdot \beta)\cdot a$.

(D) Propiedad distributiva para el producto: $(\alpha+\beta)a=\alpha\cdot a+\alpha\cdot a$.

(D) Propiedad distributiva para la suma: $\alpha\cdot (a+b) = \alpha\cdot a+\alpha\cdot b$.

(U) Elemento neutro para el producto: $\exists 1\in K: 1\cdot a=a$.

Del mismo modo podemos definir el concepto de módulo. Sea $R$ un anillo. Diremos que $(M,+,\cdot)$ es un $R$-módulo si las operaciones de suma y de producto satisfacen CANI ADDU. Por tanto, un $R$-módulo es un campo vectorial definido sobre un anillo en vez de sobre un cuerpo.

Un ejemplo de campo vectorial (sobre el cuerpo de los reales) lo encontramos, como bien sabemos, en el plano real. Es quizá más interesante el ejemplo relativo al módulo. Como mencionamos anteriormente, podemos definir sobre cada punto de una variedad $M$ el denominado espacio tangente sobre $p\in M$, que se denota por $T_p M$. Si construimos la unión disjunta de todos los espacios tangentes a todos los puntos de la variedad, encontramos el fibrado tangente (tangent bundle) $TM$. En este caso, el fibrado consta de la terna $(TM,M,\pi)$, donde $\pi: E\to M$ es una proyección, es decir, que dado $X\in TM$, $\pi(X)=p$ siendo $p$ el punto de la variedad tal que $X\in T_pM$. En este contexto, un campo vectorial sobre $M$ es una sección del fibrado, es decir, una aplicación $\sigma: M\to TM$ tal que $\pi \circ \sigma = Id_M$. Al conjunto de campos vectoriales sobre $M$ lo llamaremos $\Gamma (TM)$. Pues bien, dado que $C^{\infty}(M)$ resultaba ser un anillo, $\Gamma (TM)$ es un $C^{\infty}(M)$-módulo. Por tanto, no es un espacio vectorial.

La cuestión ahora es que existe un teorema que garantiza que todo módulo sobre un anillo divisor admite una base. En particular, por tanto, todo espacio vectorial admite una base. Sin embargo, como ya hemos señalado, $C^{\infty}(M)$ no es un anillo divisor, y por tanto $\Gamma (TM)$ no siempre admitirá una base. Para probar este resultado necesitamos adentrarnos un poco en los axiomas de la Teoría de Conjuntos, pero antes de ello dejadme añadir que las variedades que admiten una base global de campos vectoriales (que como digo, no son todas) se denominan paralelizables. En ellas sucede que el fibrado tangente es trivial, es decir, que puede ser descompuesto en el producto cartesiano $TM \cong M\times \mathbb{R}^n$, siendo $n$ la dimensión de $M$. La idea es que si la variedad es paralelizable, la base global establece un isomorfismo natural entre $TM$ y $M\times \mathbb{R}^n$.

Para el caso del círculo se verifica que $TS^1\cong S^1\times \mathbb{R}$, es decir, que el fibrado tangente al círculo es isomorfo al cilindro. Sin embargo, como hemos visto, $TS^2$ no es isomorfo a $S^2\times \mathbb{R}^2$. Existe un resultado general que dice que $TS^n\cong S^n\times\mathbb{R}^n$ si y solo si $n$ es impar. Por tanto sí que es posible peinar esferas de dimensión impar.

Un poco de Teoría de Conjuntos

 

La Teoría de Conjuntos es el pilar fundamental sobre el cual se sustenta las Matemáticas modernas, y su campo de estudio son unos entes que se denominan... conjuntos. Fue desarrollada por G. Cantor y perfeccionada y sometida a un sistema axiomático por Russell, Zermelo, Fraenkel, entre otros. El sistema axiomático que detallaremos a continuación es el sistema de Zermelo-Fraenkel (ZFC) más el axioma de elección (axiom of Choice). El motivo de separar el axioma de elección del resto de axiomas es porque es independiente de ellos, y de hecho es posible formular una teoría de conjuntos sin necesidad de él. Sin embargo, existen varios resultados fundamentales en matemáticas que precisan del axioma de elección para ser ciertos. Uno de ellos, como no podía ser de otra manera, es la demostración de que todo módulo sobre un anillo divisor admite una base.

Los axiomas ZFC tratan de definir la idea de conjunto y de pertenencia ($\in$), además de las relaciones fundamentales entre ambos objetos. Sin entrar en mucha profundidad, los axiomas son los siguientes:

1. Axioma de $\in$. $x\in y$ es una proposición si y solo si $x$ e $y$ son conjuntos. Este axioma nos permite evitar paradojas como la de Russell. Vamos a verlo. 

Supongamos que existe un conjunto $U$ que contiene a todos los conjuntos que no se contienen a sí mismos. Formalmente,

$\exists U:\forall z: (z\in U \Leftrightarrow z\notin z)$

Cabe preguntarse ahora si $U$ es un conjunto. Para ello estudiemos la proposición $U\in U$. Si ésta es cierta, entonces $U\notin U$, mas si ésta es falsa, entonces $U\notin U$ lo cual implica que $U\in U$. Por tanto, $U$ no es un conjunto, evitando así la paradoja de Russell.

2. Axioma del vacío. Existe un conjunto sin elementos: $\exists x: \forall y:y\notin x$. Es posible probar que este conjunto es único, por lo que recibe un nombre espacial: el conjunto vacío $\emptyset$.

3. Axioma de pares. Sean $x$ e $y$ dos conjuntos. Entonces existe un conjunto que contiene como elementos a $x$ e $y$.

$\forall x,y \ \exists m: \forall u:(u\in m\Leftrightarrow u=x \vee u=y)$

 

En particular, esto garantiza que si $x$ es un conjunto, existe el conjunto $\{x\}:= \{x,x\}$.

4. Axioma de la unión. Sea $x$ un conjunto. Existe un conjunto $\bigcup x$ cuyos elementos son los elementos de los elementos de $x$.

Sean $a,b$ conjuntos. Entonces existen los conjuntos $\{a\},\{b\}$ por el axioma de pares, y por tanto el conjunto $\{\{a\},\{b\}\}$. Entonces el axioma de unión garantiza que existe el conjunto $\{a,b\}$.

5. Axioma de reemplazo. Sea $R$ una relación tal que $\forall x \ \exists ! y: R(x,y)$ y $m$ un conjunto. Entonces la imagen de $m$ bajo $R$ es un conjunto. La imagen consiste en todos los $y$ tales que existe un $x\in m$ tal que $R(x,y)$. El axioma de remplazo implica el principle of restricted comprehension:

Sea $P$ un predicado de una variable y $m$ un conjunto. Entonces los $y\in m$ tales que $P(y)$ constituyen un conjunto. Éste se denota por 

$\{y\in m | P(y)\}$

6. Axioma del conjunto potencia. Sea $m$ un conjunto. Entonces existe el conjunto potencia, denotado por $\mathcal{P}(m)$, formado por todos los subconjuntos de $m$.

7. Axioma del infinito. Existe un conjunto que contiene al vacío, y para cada uno de sus elementos $y$ contiene el elemento $\{y\}$. Uno de esos conjuntos podría ser el formado por los elementos $\emptyset, \{\emptyset\}, \{\{\emptyset\}\}, ...$ Si ahora denotamos $0\equiv \emptyset$, $1\equiv \{\emptyset\}$, $2\equiv \{\{\emptyset\}\}$ y así sucesivamente, nos encontramos ante el conjunto de los números naturales, cuya existencia está garantizada por este axioma.

8. Axioma de regularidad. Todo conjunto no vacío $x$ contiene un elemento $y$ que no contiene elementos en común con $x$. En particular, ningún conjunto se puede contener a sí mismo.

Con estos ocho axiomas tenemos el sistema axiomático ZF. Como adelantamos, existe un noveno axioma independiente de los demás: el axioma de elección.

9. Axioma de elección. Sea $x$ un conjunto cuyos elementos no son vacíos y son mutuamente disjuntos. Entonces existe un conjunto $y$ que contiene exactamente un elemento de cada elemento de $x$. 

El axioma de elección es equivalente al Lema de Zorn: 

 

"Un conjunto parcialmente ordenado $P$ tal que todos sus subconjuntos totalmente ordenados poseen una cota superior en $P$ contiene un elemento maximal"

Antes de explicar el contenido de este lema, es necesario añadir que Zermelo trató de probarlo a partir del resto de axiomas, pero los Teoremas de Incompletitud de Gödel implican que el lema de Zorn no es demostrable a partir de los axiomas ZF. Por tanto se incorporó como noveno axioma. A continuación vamos a explicar el contenido del lema, cuya demostración a partir del axioma de elección podéis encontrar en el siguiente enlace.

1. Un conjunto $(P,\le)$ es parcialmente ordenado si, para todos $a,b,c\in P$ se satisfacen las siguientes propiedades:

- Reflexividad: $a\le a$.

- Antisimetría: $(a\le b \wedge b\le a) \Rightarrow a=b$.

- Transitividad: $(a\le b \wedge b\le c) \Rightarrow a\le c$.

2. Un conjunto $(T,\le)$ es totalmente ordenado si, para todos $a,b,c\in P$ se satisfacen las propiedades de:

 

- Antisimetría: $(a\le b \wedge b\le a) \Rightarrow a=b$.

- Transitividad: $(a\le b \wedge b\le c) \Rightarrow a\le c$.

- Totalidad: $a\le b$ o $b\le a$.

La diferencia entre ambas definiciones radica, por tanto, en la reflexividad (que no es requerida para un conjunto totalmente ordenado, pero sí por el parcialmente ordenado) y la totalidad.

3. Cota superior: $u\in P$ es una cota superior de un subconjunto $T\subseteq P$ si para todo $t\in T: t\le u$.

4. Elemento maximal: $m$ es un elemento maximal de $P$ si no existe $x\in P$ tal que $m\le x$.

Muy bien, llega el momento de enunciar y demostrar el resultado clave de esta entrada, y es que todo módulo sobre un anillo de división admite una base. Recordemos que dado un $R$-módulo $V$, una base $B$ (en el sentido de Hamel) es un subconjunto $B\subseteq V$ tal que

 

(i) Todo subconjunto finito $\{b_1,...,b_N\}\subseteq B$ es linealmente independiente, es decir que $\lambda^i b_i = 0 \Rightarrow \lambda^i = 0 \ \forall i=1,...,N$.

 

(ii) Para todo $v\in V$ existen $v^1,...,v^M\in R$ y $b_1,...,b_M\in B$ tales que $v=v^ib_i$ (empleamos el convenio de sumación de Einstein).

 

Ahora sí, la demostración se organizará en cinco pasos:

(a) Sea $V$ un módulo sobre un anillo divisor $D$. Sea $S$ un sistema generador de $V$, es decir, que para todo $v\in V$ existan $e_1,...,e_N\in S$ y $v^1,...,v^N\in D$ tales que $v=v^a e_a$. Ciertamente $S$ existe, pues en el peor de los casos podemos tomar $S$ como el módulo entero. Nótese también que $S$ no constituye una base de $V$.

(b) Definimos un conjunto parcialmente ordenado, $(P,\le)$ mediante el conjunto

$P:=\{U\in \mathcal{P}(S) | U \ \text{es linealmente independiente}\}$

y la relación $\le\ \equiv\ \subseteq$. Entendemos que un conjunto es linealmente independiente si todo subconjunto finito de éste lo es. Ciertamente, por el axioma de reemplazo y el del conjunto potencia, $P$ es un conjunto y evidentemente la relación $\subseteq$ es parcial.

(c) Sea $T$ cualquier subconjunto totalmente ordenado de $P$. Entonces la unión $\bigcup T$ es una cota superior de $T$. Por el lema de Zorn, $P$ tiene entonces un elemento maximal $B$, que por construcción es el subconjunto de $S$ linealmente independiente más grande.

(d) El siguiente paso es probar que $B$ genera $S$. Sea $v\in S$. Dado que $B$ es maximal, $B\cup \{v\}$ es linealmente dependiente, por lo que existen $e_1,...,e_N\in B$ y $a^1,...,a^N\in D$, además de un $a\in D$, tales que $a^ie_i + av = 0$ donde $a\neq 0$ y no todos los $a^i$ son nulos. Es evidente que $a\neq 0$ porque $B$ es linealmente independiente. Como $D$ es divisor, existe $a^{-1}\in D$ tal que $a\cdot a^{-1}=1$. Por tanto $v=-a^{-1} a^i e_i$, lo cual prueba que $B$ genera $S$.

(e) Por último, dado que por hipótesis $V=span_D(S)$ y acabamos de ver que $S=span_D(B)$, entonces $V=span_D(B)$. Como $B$ es linealmente independiente y además genera $V$, $B$ es una base de $V$.

 

Como queríamos demostrar, todo módulo sobre un anillo de división admite una base. Nótese que el axioma de elección (escrito equivalentemente en términos del Lema de Zorn) ha jugado un papel determinante en esta demostración, así como el hecho de que $D$ sea un anillo de división.

Finalmente, el hecho de que el conjunto de funciones infinitamente diferenciables sobre la variedad, $C^{\infty}(M)$, no sea un anillo de división implica que no está garantizado que siempre exista una base global de campos vectoriales sobre una variedad. Si esto ocurre, como en el toro, la variedad es paralelizable y su fibrado tangente es trivial. Si no, como en las esferas de dimensión par, no es posible encontrar un campo vectorial que no se anule en algún punto. Y éste es el motivo por el cual no es posible peinar una esfera.

Conclusiones

 

En esta entrada hemos entendido de forma visual que existen superficies (o en general, variedades) que admiten un campo vectorial que no se anule en ningún punto y otras que no. Nos hemos referido a ellas como "que se pueden (o no) peinar". El hecho de que no esté garantizada la exisencia de una base global de campos vectoriales se debe a que el conjunto de campos sobre una variedad no tiene estructura de espacio vectorial, si no que es un módulo sobre un anillo no divisor. Con un poco de álgebra y algunas nociones sobre teoría de conjuntos, hemos demostrado por qué no está garantizada la existencia de dicha base.

Referencias

- Teorema de la bola de pelo

- Fibrado y fibrado tangente

- Variedad paralelizable

- Lema de Zorn

- Axiomas de la teoría de conjuntos

- Curso de Geometría Diferencial de Frederic Schuller

- Lectures on geometrical anatomy of theoretical physics de Frederic Schuller

- Cuerpo, anillo y módulo.

Energía gravitatoria

En Mecánica Clásica entendemos la energía como aquel ente capaz de realizar un trabajo. Si por ejemplo consideramos un campo de fuerzas conservativas, es decir que posean un potencial, podemos definir una energía potencial asociada a dicho campo, que se interpretaría como aquella cantidad de energía necesaria para desplazar una partícula hasta el infinito (o hasta tierra, es decir, donde el campo se anule).

Potencial gravitatorio creado por una distribución esférica de masa $M$.

Consideremos la gravitación Newtoniana, donde el campo de fuerzas viene definido por la Ley de la Gravitación Universal:

$$ \vec F = - G \frac{m_1 m_2}{r^3} \vec r$$

siendo $G$ la constante de la gravitación universal, $m_1$ y $m_2$ las masas de las partículas en interacción y $\vec r$ el vector que las une. El campo es conservativo, pues proviene del potencial gravitatorio 

$$ V = - G \frac{m_1 m_2}{r} $$

ya que $\vec F = -\nabla V$. La energía potencial se define como el potencial por unidad de masa. Si $M=m_1$ es la masa de la partícula que crea el campo y $m_2$ la que lo "siente", la energía potencial será 

$$E = - G \frac{M}{r}$$

La interpretación física es que el valor numérico de $E$ en $r=r_0$ es la energía necesaria para llevar la partícula de $r=r_0$ hasta el infinito, donde no hay influencia gravitatoria. En este sentido, hemos encontrado una expresión local para la energía gravitatoria. Sin embargo, vamos a ver cómo todo se vuelve más complicado cuando nos adentramos en las fauces de la Relatividad General.

Principio de Equivalencia

Recordemos que, según la Segunda Ley de Newton, la fuerza y la aceleración que experimenta un cuerpo de masa $m$ están relacionadas por 

$$\vec F= m \vec a$$

Por otro lado, hemos visto que la fuerza gravitatoria también depende de la masa $m$ de los cuerpos en interacción. La pregunta es, ¿son estas dos masas la misma? Esto es lo que se conoce como Principio de Equivalencia de Galileo.

En principio no tendría por qué. Fijémonos por ejemplo en la Ley de Coulomb, donde la fuerza electrostática depende de la carga $q$ de la partícula, no de la masa. De hecho, dos partículas de igual masa pero distinta carga acelerarán de forma diferente en presencia de un campo eléctrico. Esto es radicalmente distinto a lo que ocurre con el campo gravitatorio, en el que todos los cuerpos caen con la misma aceleración. ¿Qué tiene de especial la Gravitación?

A lo largo de la Historia ha habido multitud de experimentos para tratar de discernir si en efecto la masa gravitatoria (la de la Ley de la Gravitación Universal) es la misma que la masa inercial (la de la Segunda Ley de Newton). Uno de los más famosos fue el ideado por Lóránd von Eötvös, en el que aprovechó la rotación de la Tierra y la aceleración centrífuga correspondiente. En dicha experiencia y en sucesivas mejoras, se ha logrado probar que ambas masas son iguales con un error menor a $10^{-13}$ (en 1999). Actualmente la sonda espacial MicroSCOPE ha logrado llegar a cotas de $10^{-15}$, y se espera que el satélite STEP alcance hasta $10^{-18}$. Así pues, el Principio de Equivalencia de Galileo tiene una gran base experimental. Ahora bien, ¿qué conclusiones podemos obtener de él?

El Principio de Equivalencia de Galileo parece apuntar a que, de algún modo, un sistema de referencia acelerado es equivalente a uno inercial en presencia de un campo gravitatorio. Dado que el campo gravitatorio no es uniforme, esta equivalencia es sólo local. En este sentido, somos capaces de anular el efecto del campo gravitatorio dejándonos caer en él.

El ejemplo típico, atribuido a Einstein, es el del ascensor. Si consideramos un ascensor que asciende con velocidad uniforme y dejamos caer un objeto, éste impactará contra el suelo del ascensor por efecto de la gravedad. Si repetimos el experimento en el espacio (sin gravedad) pero con un ascensor que se mueva de forma acelerada, el resultado va a ser el mismo. Análogamente, la Física en un ascensor inercial en ausencia de gravedad es la misma (localmente) a la que experimentaríamos en un ascensor en caída libre en presencia de un campo gravitatorio. Si en esta situación soltásemos un objeto, éste caería con nosotros, y lo percibiríamos "suspendido" ante nuestros ojos, como un sistema inercial en Relatividad Especial.

Einstein elevó el Principio de Equivalencia a la categoría de postulado para su Teoría de la Relatividad General. Dicho postulado reza:

Todas las leyes de la Física (salvo la gravitación) son las mismas, a escalas suficientemente locales, en un sistema en caída libre en presencia de un campo gravitatorio o en un sistema inercial en ausencia de gravedad.

Una versión alternativa es:

Todas las leyes de la Física (salvo la gravedad) son iguales, localmente, en un sistema inercial en presencia de un campo gravitatorio y en un sistema de referencia acelerado en ausencia de gravedad.

La principal consecuencia de este Postulado es que la gravedad ya no es una fuerza, si no que se trata de un efecto debido a la Geometría del espacio y del tiempo. Y una consecuencia secundaria es la imposibilidad de definir el concepto de energía local gravitatoria en Relatividad General. Veamos por qué.

Energía local gravitatoria

Recordemos que el Principio de Equivalencia nos lleva a abandonar toda esperanza de poder "medir el campo gravitatorio", al igual que Dante al descender al Inferno:

" Lasciate ogni speranza, voi ch'entrate "

Inferno, La Divina Commedia, Dante Alighieri

Esto es debido a que el valor del campo (la métrica) toma valores diferentes en sistemas de referencia distintos. Por ejemplo, un observador en caída libre (coordenadas gaussinas), observa localmente la métrica de Minkowski, es decir, no siente la gravedad. En el límite newtoniano, la energía asociada al campo viene dada por el laplaciano del potencial gravitatorio, de modo que en Relatividad General esperaríamos que ésta dependiese de la métrica $g$ y sus primeras derivadas. Pero por el Principio de Equivalencia, la energía tomaría valores distintos en diferentes sistemas coordenados. Este es el motivo por el cual no se puede definir un tensor local de energía gravitatoria.

Sin embargo, sí que es posible construir un pseudo-tensor local, como por ejemplo el de Landau-Lifshitz. Este objeto no es tensorial, pues se anula en unos sistemas y no en otros, por lo que capta la esencia fundamental del Principio de Equivalencia. Además, a partir de él se pueden construir unas cantidades (masa ADM o momento ADM, en honor a Arnowitt-Deser-Misner, sus descubridores) conservados cuya interpretación es una medida global de la energía gravitatoria. La base matemática para introducir las formas de Landau-Lifshitz es bastante complicada, por lo que definiremos la masa ADM desde otra vía.

Desde los años 60 del siglo pasado se sabe que la formulación hamiltoniana de la Relatividad General (GR) es equivalente a la planteada por Albert Einstein en su teoría. A grandes rasgos, el Hamiltoniano es suma de dos términos: la ligadura hamiltoniana y la ligadura vectorial. Este formalismo canónico se sustenta en una descomposición 3+1 de la GR. Sin embargo, para normalizar el valor de la acción en GR es necesario añadir ciertos términos de frontera al hamiltoniano. Pues bien, precisamente uno de esos términos es la energía ADM:

$$E = \frac{1}{2}\int n^k(\partial_i h_{ik}-\partial_k h_{jj}) dS$$

donde la integral se realiza en la esfera del infinito, cuyo vector normal es $n$ y $h$ denota la métrica asintóticamente plana. Esta energía ADM obtenida desde el formalismo canónico es la misma que se encuentra a través del pseudo-tensor de Landau-Lifshitz.

El ejemplo clásico no trivial es la energía ADM para la métrica de Schwarzschild en coordenadas isotrópicas. Un sencillo cálculo nos permite comprobar que dicha energía es igual a la masa fuente del campo gravitatorio. De esta forma podemos interpretar la energía ADM como una medida global de la energía de campo gravitatorio en Relatividad General. Si añadimos dicha energía como término de frontera al hamiltoniano, el valor numérico de éste resulta ser la energía ADM, recuperando así la noción de que el hamiltoniano es la energía del sistema.

Conclusiones

 

Según hemos visto, el Principio de Equivalencia nos obliga a abandonar la idea de poder medir el campo gravitatorio, y con ello a ser capaces de definir una medida local de energía gravitatoria. Sin embargo, sí que se puede definir una medida global de energía, asociada a la totalidad del campo. Dicha energía (ADM) se puede obtener desde una vía puramente geométrica (a partir de las formas de Landau-Lifshitz) o desde un planteamiento hamiltoniano de la Relatividad General.

Referencias

 

- R. Arnowitt, S. Deser, C. W. Misner, "Gravitation: An introduction to current research. The dynamics of General Relativity". John Wiley, Sons Inc., New York, London (1962).

- R. M. Wald, "General Relativity", The University of Chicago Press, Chicago and London, (1984).

- Y. Choquet-Bruhat, "General Relativity and the Einstein Equations". Oxford Mathematical Monographs, (2009).

 

Sobre la imposibilidad de la cuadratura del círculo

Muchos han sido los intentos de cuadrar un círculo con las "reglas clásicas de la antigüedad", es decir, construir con "regla y compás" un cuadrado de área igual a un círculo dado. Desde hace 150 años se sabe que es una tarea completamente imposible, al igual que muchos otros, como la trisección del ángulo o la duplicación del cubo (los tres problemas délicos). ¿Qué relación tiene la cuadratura del círculo con la trascendencia de $\pi$? ¡Comencemos!

Primero vamos a probar que el número $\pi$ es irracional y trascendente (sobre $\mathbb{Q}$, que lo omitiré en adelante). Este resultado es imprescindible para lo que después desarrollaremos.

Proposición: Todo número trascendente es irracional.

Demostración: supongamos que un número trascendente $p$ es racional. Entonces $p=\displaystyle\frac{a}{b}$ para ciertos enteros $a$ y $b$. Construímos el polinomio $p(x)=bx-a$, y como tiene por raíz a $p$, entonces es algebraico. Habiendo llegado a una contradicción, es claro que todo número trascendente es irracional. Por ello nos limitaremos a demostrar la trascendencia de $\pi$.

Una vez demostrada la trascendencia de $\pi$, veremos qué tiene que ver con la imposibilidad de cuadrar un círculo con regla y compás. Finalmente estudiaremos unas cuantas consecuencias y teoremas más.

1. Teorema de Lindemann-Weierstrass

Hermite (sí, el de los polinomios) fue el primero en probar que cualquier potencia racional de $e$ es trascendente, demostrando así que el propio $e$ es trascendente. Nueve años después, Lindemann lo generalizó diciendo que $e$ elevado a cualquier número algebraico es trascendente. Sin conocer la prueba de Lindemann, el español José Echegaray llegó al mismo resultado en 1886. El artículo lo puedes encontrar aquí.

Nosotros vamos a demostrar el caso más general del teorema, para luego particularizar al resultado que nos concierne. Bueno, vamos a ello:

Lema (A): dados $c(i) \ \neq 0 \ \forall i\in\mathbb{Z}\cap [1,r]$ sean ${y(k)_1,..., y(k)_{m(k)}}$   las raíces de un polinomio con coeficientes $T_k(x)=v(k) x^{m(k)}+...+u(k)$ $\forall k\in[1,r]$ enteros y con $u(k), v(k)\neq 0$. Entonces si $y(k)_i\neq y(u)_v$ con $(k, i)\neq (u, v)$ se tiene que $\sum_{i=1}^r{c(i)(e^{y(i)_i}+...+e^{y(i)_{m(i)}})}\neq 0$.

Demostración: en primer lugar la expresión final del enunciado puede ser escrita como 

$S=\sum_{k=1}^n\beta_k e^{\alpha_k}\neq 0$

donde $n_0=0$, $n=n_r$, $n_i=\sum_{k=1}^i m(k)$ con $i=1, …, r$, $\alpha_{n_i+j}=y(i+1)_j$ con $0\leq i\leq r$, $1\leq j\leq m(i)$ y $\beta_{n_i+j}=c(i+1)$. Supongamos que $S=0$ para llegar a una contradicción. Sea ahora 

$f_i(x):=\frac{l^{np}(x-\alpha_1)^p...(x-\alpha_n)^p}{(x-\alpha_i)}$

con $l$ entero y construyamos $I_i(s)=\int_0^s e^{s-x}f_i(x) dx=e^s\sum_{j=0}^{np-1}f_i^{(j)}(0)-\sum_{j=0}^{np-1}f_i^{(j)}(s)$ integrando por partes. En caso de que $s$ sea complejo integramos en un contorno cerrado que pase por la recta real y usamos el Teorema de Cauchy. Ahora evaluemos la suma

$J_i=\sum_{k=1}^n \beta_k I_i(\alpha_k)=\sum_{j=0}^{np-1}f_i^{(j)}(0)\sum_{k=1}^n\beta_ke^{\alpha_k}-\sum_{k=1}^n\sum_{j=0}^{np-1}\beta_k f_i^{(j)}(\alpha_k)$ por lo que $J_i=-\sum_{k=1}^n\sum_{j=0}^{np-1}\beta_kf_i^{(j)}(\alpha_k)$ donde en la última igualdad hemos usado la hipótesis del absurdo.

Si $j\geq p$ entonces $f_i^{(j)}(\alpha_k)$ es un entero algebraico múltiplo de $p!$. Si $j<p-1$ es claro que $f_i^{(j)}(\alpha_k)=0$ y si $j=p-1$ y $k=i$ entonces $f_i^{(j)}(\alpha_k)=l^{np}(p-1)!\prod_{i\neq k}(\alpha_i-\alpha_k)$. Este entero no es divisible por $p$ haciendo uso del Pequeño Teorema de Fermat, como puedes comprobar en la bibligrafía. Por tanto $J_i$ es divisible por $(p-1)!$. Ahora, reescribiendo $J_i$ como sigue

$J_i=-\sum_{j=0}^{np-1}\sum_{t=0}^{r-1}c(t+1)(f_i^{(j)}(\alpha_{n_t+1})++f_i^{(j)}(\alpha_{n_{t+1}}))$

Usando el Teorema Fundamental de polinomios simétricos, se puede probar que $J_i$ es un polinomio $G(\alpha_i)$, por lo que $|J_1...J_n|$ es un entero divisible por $(p-1)!^n$. La contradicción llega del hecho de que $|I(a_k)|\leq |a_k| e^{|a_k|}F_i{|a_k|}$ donde $F_i(x)$ es el polinomio cuyos coeficientes son los de $f_i(x)$ en valor absoluto. Pero entonces $J_i(|a_k|)\leq\sum_{k=1}^n|a_k\beta_k|e^{|a_k|}F_i(|a_k|)$ por lo que de alguna forma $|J_1...J_n|$ está acotado superiormente por cierto $N^p$, lo cual contradice la desigualdad anterior ya que $p$ es arbitrario y la cota inferior supera a la superior para $p$ suficientemente grande.


Otro Lema (B): si $b(1),...,b(n)$ son naturales y $y(1),...,y(n)$ son algebraicos y diferentes, entonces $b(1)e^{y(1)}+...+b(n)e^{y(n)}\neq 0$.

Prueba: construyamos un polinomio con coeficientes enteros cuyas raíces sean $y(1),...,y(n),y(n+1),...y(N)$ y definamos $b(n+1)=…=b(N)=0$. Si suponemos que el enunciado es falso, es claro que 

$\prod_{\sigma\in S_N}(b(1)e^{y(\sigma(1)}+...+b(N)e^{y(\sigma(N)})=0$

donde estamos considerando todas las permutaciones. Pero si expandimos ese productorio nos aparecen términos en exponenciales simétricas y al agrupar nos vamos a encontrar con una suma semejante a la del enunciado del lema A. Puede probarse que se satisfacen dichas hipótesis, lo cual es contradictorio y prueba el lema B.

Teorema de Lindemann-Weierstrass: si $a_1,...,a_n$ son números algebraicos no nulos y $\beta_1,...,\beta_n$ son números algebraicos distintos, entonces $a_1e^{\beta_1}+...+a_ne^{\beta_n}\neq 0$.

Demostración: se prueba de forma muy parecida al Lema B.

La prueba que dio Lindemann originalmente de que $\pi$ es trascendente os la dejo en la bibliografía. Es menos general pero es suficiente para lo que necesitamos en esta entrada. De hecho simplemente con los lemas A y B podríamos probar la trascendencia e irracionalidad de $\pi$ y de $e$.

La trascendencia de $e$ ya fue probada en una entrada anterior, que puedes leer aquí. De hecho es trivial sin más que ver el enunciado del lema B, ya que si $e$ fuese algebraico la igualdad sería cero para ciertos coeficientes. 

Ahora bien, si $\pi$ fuera algebraico, la ecuación $e^{i\pi}+1=0$ contradeciría el Lema B, por consiguiente acabamos de demostrar que el número $\pi$ es trascendental. Ahora vamos a estudiar la relación entre la trascendencia y el hecho de que el número $\pi$ no sea construible.

2. Imposibilidad de cuadrar un círculo

En primer lugar os remito a la bibliografía para entender bien qué queremos decir con que un punto sea o no construible. Para el tema que nos concierne, es suficiente que entendáis que si $a$ y $b$ son dos puntos construibles, entonces su cociente es construible. Esto será clave para demostrar que es imposible cuadrar el círculo. Vayamos ahora a por un teorema, que tengo algo de mono.

Un número es construible sí y sólo sí es algebraico y su polinomio mínimo irreducible sobre $\mathbb{Q}$ es potencia de 2.

La demostración la puedes encontrar en el libro "What is mathematics?" que os dejo en la bibliografía, entre las páginas 127 y 140. La idea es simple y voy a tratar de ilustrarla.

Primero define un "number field" como un conjunto de números cerrado bajo operaciones racionales (suma, resta, producto y división). Llama $F_0$ al rational field y $F_1$ al irracional, que lo obtiene a partir de $F_=$. Obviamente ambos son construibles de forma muy sencillita (os vuelvo a remitir al artículo de Gaussianos). Poco a poco construye nuevos $F's$ a partir de los anteriores y observa qué números son construibles. Por ejemplo, los números de $F_1$ vienen de ecuaciones de segundo grado, los de $F_3$ de cuarto grado y así sucesivamente. Por tanto los números algebraicos son los únicos construibles. Además 


Supongamos que es posible cuadrar el círculo con regla y compás. Esto equivale a decir que $R$ y $L$ son construibles, siendo $R$ el radio del círculo y $L$ el lado del cuadrado. Como $\pi R^2=L^2$ entonces $\sqrt{\pi}=L/R$ es construible por serlo $R$ y $L$. Pero esto es falso por ser $\pi$ trascendental. Con lo cual queda probada la imposibilidad de cuadrar el círculo.


3. Otros problemas délicos 


Además de la imposibilidad de cuadrar el círculo, existen otros dos problemas clásicos que se han demostrado imposibles.

Duplicación del cubo: no es posible porque el polinomio mínimo irreducible de $\sqrt[3]{2}$ es $x^3-2=0$ y 3 no es múltilplo de 2.

Trisección del ángulo: algunos ángulos sí se pueden trisecar, pero no es posible en general. En el artículo de Gaussianos de la bibliografía lo tiene hecho con el ángulo de 60º.



4. Curiosidades


Hay otro teorema, el de Gelfond-Schneider, que garantiza que $a^b$ es trascendente si $a$ y $b$ son algebraicos y $b$ es irracional. Junto con el Teorema de Lindemann sería consecuencia de la Conjetura de Schanuel, que no es más que eso, una conjetura.

De hecho, el teorema de Gelfond es el resultado del séptimo problema de Hilbert, una lista de 23 problemas matemáticos enunciada por Hilbert a principios del siglo pasado, de los cuales se han resuelto 9. 



5. Conclusiones

La idea básica de esta entrada era probar que la cuadratura del círculo es imposible. Para ello hemos definido lo que es una construcción clásica con regla y compás, y hemos demostrado que sólo podemos construir números algebraicos que sean raíz de un polinomio irreducible de grado $2^n$ con $n$ natural. Habiendo probado que $\pi$ es trascendente gracias al Teorema de Lindemann-Weierstrass, hemos conseguido nuestro objetivo.

Bibliografía

- https://es.wikipedia.org/wiki/N%C3%BAmero_trascendente

- https://en.wikipedia.org/wiki/Lindemann–Weierstrass_theorem (Teorema de Lindemann)

-  http://gaussianos.com/echegaray-y-la-trascendencia-de-pi

- http://gaussianos.com/como-demostrar-que-%CF%80-pi-es-trascendente/

- http://gaussianos.com/construcciones-con-regla-y-compas-i-introduccion-y-primeras-construcciones/ (Construcciones clásicas con regla y compás)

- http://gaussianos.com/construcciones-con-regla-y-compas-ii-los-problemas-delicos/

- http://mimosa.pntic.mec.es/jgomez53/matema/conocer/numpi_lindemann.htm

- http://gaussianos.com/quien-dijo-que-la-cuadratura-del-circulo-era-imposible/

- http://www.cimat.mx/~ibrahim/LOTra_JIVG.pdf

- https://es.wikipedia.org/wiki/Problemas_de_Hilbert (Problemas de Hilbert)

- https://es.wikipedia.org/wiki/Teorema_de_Gelfond-Schneider

- What is mathematics? Courant & Robbins (los números algebraicos son los únicos construibles, pág 127-140)

- http://rodin.uca.es/xmlui/bitstream/handle/10498/7163/33925574.pdf (José Echegaray)

- http://sixthform.info/maths/files/pitrans.pdf (Más sobre la trascendencia de $\pi$)

Las leyes de Newton y la curvatura del espaciotiempo

Todos hemos oído hablar de las leyes de Newton desde pequeños. La primera de ellas nos dice cómo se mueve una partícula sobre la que no actúa ninguna fuerza, la segunda habla del efecto que produce la fuerza sobre la trayectoria, y la tercera es la ley de acción y reacción. En esta entrada nos vamos a centrar sólo en las dos primeras, que rezan así:

1ª Ley: un cuerpo sobre el que no actúa ninguna fuerza se mueve uniformemente y en línea recta.

2ª Ley: la desviación que sufre un cuerpo de moverse "libremente", es decir, uniformemente y en línea recta, es proporcional a la fuerza que actúa sobre él.

En un sentido clásico, la primera ley nos define lo que es un sistema inercial, concepto clave, pues sólo en estos sistemas pueden aplicarse las otras dos leyes. Pero ya vemos aquí cierto argumento circular: ¿Cómo sabemos que sobre un cuerpo no actúan fuerzas?

De hecho, la fuerza de la gravedad es de alcance infinito, lo que lleva a pensar que la primera ley de Newton carece de significado práctico. ¿Cómo podemos lidiar con la 1ª Ley y con el hecho de que exista la gravedad? Muy sencillo, exigiendo que la gravedad no sea una fuerza sino algo distinto.

Desde un punto de vista geométrico, la 1ª Ley nos define lo que es una línea recta, es decir, nos define la curvatura de nuestro espacio (tiempo), y la 2ª nos informa de la desviación de las trayectorias como consecuencia de las fuerzas.

Para entender perfectamente la Física de esta entrada necesitamos cierto background matemático que pasaré a resumir a continuación.

1. Nociones básicas de geometría.

Sea $(M,\theta,A)$ una variedad topológica diferenciable de dimensión $n$. Esto no es más que dotar a un conjunto $M$ de una topología $\theta$, osea, definir sobre ese conjunto lo que es un abierto $U$ y exigir que sea localmente homeomorfo a $\mathbb{R}^n$, es decir, que para cada abierto $U\subset M$ exista un homeomorfismo $x: U\longrightarrow \mathbb{R}^n$ biyectivo, continuo, invertible y con inversa continua. A la función $x$ se la llama "función coordenada" o "coordenadas".

Esto no es nada del otro mundo. Pensad que cada punto $p$ de una esfera puede ser representado por dos coordenadas, $\theta$ y $\phi$, que representan a la esfera como un abierto de $\mathbb{R}^2$ de forma local.

Sobre cada $p\in M$ puedo construir un espacio vectorial llamado espacio tangente de la siguiente forma:

$T_pM := span\{\partial/\partial x^1, …, \partial/\partial x^n\}$

Cada $X_p\in T_pM$ es una aplicación $X_p : C^{\infty}(M)\longrightarrow \mathbb{R}$ que de cada función sobre la variedad me dice su "derivada direccional" $X_p(f):= X^i\partial_i f$, donde entendemos que $\partial_i f := \partial/\partial x^i (f\circ x^{-1})$.

Ahora puedo construir el fibrado tangente, $TM$, como la unión disjunta de todos los espacios tangentes a cada punto de la variedad. Ciertamente puedo proyectar la topología de $M$ sobre $TM$ haciendo que $TM$ sea una variedad diferenciable. Con estas estructuras puedo definir un campo vectorial $X$ como una aplicación $X:M\longrightarrow TM$ tal que $X\circ \pi=Id$ con $\pi$ la proyección canónica de $TM$ sobre $M$. El conjunto de campos vectoriales sobre el anillo $C^{\infty}(M)$, $\Gamma(TM)$, tiene estructura de $C^{\infty}(M)$-module, pues $C^{\infty}(M)$ es un anillo, no un cuerpo. Esto va a implicar que no tiene por qué existir una base de $\Gamma(TM)$ global (pero sí local, obviamente). 

Ahora que sé derivar funciones sobre variedades, $\nabla_X f := X(f)$, me interesa saber derivar tensores en general. Para ello construyo el operador $\nabla_X$ con una serie de propiedades (imponiendo que el resultado sea tensorial) y me doy cuenta que tengo bastante libertad a la hora de escoger su funcionamiento. En particular puedo escoger arbitrariamente lo que se denomina la conexión $\Gamma^i_{j k}:=dx^i(\nabla_k \partial_j)$ para así "definir" cómo actúan sobre campos vectoriales. En cierto sentido las $\Gamma$'s portan información sobre lo que entendemos por "paralelismo" sobre la variedad.

Lo realmente bonito es el hecho de que la conexión no es un tensor, es decir, las funciones $\Gamma^i_{j k}$, no transforman como un tensor, lo cual va a ser muy relevante posteriormente. Añado en este punto que la parte antisimétrica de la conexión sí que transforma como un tensor: la torsión.

Debido a que no transforman como tensores, punto a punto puedo escoger un cambio de coordenadas que me anulen la conexión (la parte no tensorial), pero en general no puedo anular la conexión en todo mi espacio, eso dependerá de la curvatura de la misma. Vamos ahora a definir qué es eso de la curvatura.

Sea $\gamma:\mathbb{R}\longrightarrow M$ una curva suave y sea $V$ el campo de vectores tangentes a la curva sobre la curva (en realidad sólo necesito vectores punto a punto). Un vector $X$ es transportado a lo largo de la curva si $\nabla_V X=0$. Esto no es más que ir arrastrando el vector sobre la curva sin modificar sus componentes (transporte paralelo). 

Un vector transportado paralelamente a lo largo de la curva 

Cuando en una curva su vector tangente es transportado paralelamente a lo largo de ella misma, decimos que esa curva es una geodésica (afín). Vamos a calcular en coordenadas la ecuación de una geodésica. Para ello dada la curva $\gamma$ parametrizada por $t\in\mathbb{R}$ definimos su vector tangente en un punto $p=\gamma(t_0)$ como $V(f):=d/dt (f\circ \gamma)(t_0)$, de modo que en coordenadas, $V=\dot{\gamma^i}\partial_i $. Por tanto, la ecuación de la geodésica en componentes es 

$(\nabla_{\dot{\gamma^i}\partial_i}(\dot\gamma^n\partial_n))^m=\ddot\gamma^m+\Gamma^m_{a b}\dot{\gamma}^a\dot\gamma^b=0$

Las curvas que siguen las partículas libres ahora dependen de la conexión. Para una variedad plana en cartesianas, las $\Gamma$'s son nulas, y recuperamos el movimiento rectilíneo uniforme, pero en variedades curvas con conexiones arbitrarias la cosa ya no es tan sencilla.

Si has estudiado geometría diferencial sobre superficies en $\mathbb{R}^3$ habrás estudiado las geodésicas métricas como las que minimizan la distancia sobre la superficie. Es sencillo probar que usando la conexión usual de Levi-Civita, esa definición es equivalente a la nuestra. En ese caso, las geodésicas son las curvas tales que su vector de curvatura es normal a la superficie a lo largo de toda la curva, osea que su curvatura geodésica es nula. Habrás estudiado también la derivada "intrínseca" a lo largo de una curva como la derivada usual a la que le restamos la componente normal. Pues es equivalente (Levi-Civita). Nótese que nosotros no hemos dotado aún de una métrica a nuestra variedad y que diferenciamos, en principio, geodésicas métricas (minimizan la distancia) de geodésicas afines (se autotransportan paralelamente).

Definimos ahora el tensor de Riemann como 

$Riem(\omega,Z,X,Y):=\omega(\nabla_X\nabla_Y Z-\nabla_Y\nabla_X Z-\nabla_{[X,Y]} Z)$ 

que se puede entender como la curvatura de la variedad. Podemos escribirlo en coordenadas en función de la conexión y sus derivadas, por lo que en una variedad curva es imposible eliminar la conexión con un simple cambio de coordenadas, ya que $Riem$ es un tensor. Finalmente se define el tensor de Ricci contrayendo el primer y el tercer índice de $Riem$, y el escalar de Ricci contrayendo el tensor de Ricci con la métrica.

Para aclarar un poco las ideas, supongamos dos aviones que se dirigen hacia el polo norte. Uno despega desde Ecuador y otro desde Guinea. A medida que avanzan, los dos aviones tienden a acercarse. Si los pasajeros de ambos aparatos no saben que la Tierra es esférica, postularán que hay una misteriosa fuerza que los atrae. Pero alguien que sepa que la Tierra es redonda, atribuirá dicho acercamiento a un efecto de la curvatura terrestre. Esto es precisamente lo que vamos a hacer con la gravedad, salvando las distancias.

2. La motivación de Laplace

En esta sección vamos a intentar abandonar la idea de la gravedad como una fuerza para intentar entenderla como consecuencia de un espaciotiempo curvado. Esta motivación surge del principio de equivalencia, es decir, de la idea de que todas las partículas se aceleran igual independientemente de su masa. Lo que intentó Laplace fue codificar el campo gravitatorio de tal manera que la 2ª Ley de Newton para la gravedad tomase la forma de una geodésica. Pero eso es imposible, ya que la fuerza de la gravedad sólo depende de las posiciones, no de las velocidades, y en la ecuación de la geodésica intervienen las velocidades.

El problema de fondo es que hasta ahora nuestras curvas dependen de la parametrización. Para librarnos de ella simplemente pensemos en el tiempo como una coordenada más. Simplemente eso. Hasta ahora una curva era de la forma $(x^1(t), x^2(t), x^3(t))$. Ahora es una aplicación hacia $\mathbb{R}^4$ del tipo $(x^0(t)\equiv t, x^1(t), x^2(t), x^3(t))$. Entonces la ecuación de una partícula en un campo gravitatorio, teniendo en cuenta el principio de equivalencia,

$\ddot x^a-f^a(x(t))=0$

es equivalente a la ecuación de la geodésica en una variedad de dimensión 4 dotada de una conexión nula salvo los términos $\Gamma^{\alpha}_{0 0}=-f^{\alpha}(x(t))$ con $\alpha\neq 0$, ya que $\dot{x}^0=1$.

$\ddot{x}^a+\Gamma^a_{b c}\dot{x}^b\dot x^c=0$

Ciertamente existe curvatura, y no es un artificio por una extraña elección de coordenadas. Basta calcularse el tensor de Riemann para comprobarlo. En otras coordenadas donde espacio y tiempo se entremezclen, la conexión tomará formas extrañas, pero tomando $x^0=t$ (atlas estratificado) queda así de sencilla. La curvatura es por tanto temporal y la fuerza de la gravedad ahora no es más que un efecto de la curvatura del espaciotiempo de Newton. De este modo la 1ª Ley funciona y nos define la geometría de nuestro espacio. 

Como curiosidad podemos calcular la componente (0, 0) del tensor de Ricci, y usando la ecuación de Poisson para el campo gravitatorio, vemos que en cartesianas $Ri_{0 0}=-\partial_a f^a =4\pi G \rho$. Esto es una maravilla. ¡La curvatura de la variedad viene codificada por la densidad de materia! Recuerda que estamos en mecánica Newtoniana, no hemos mencionado nada de Relatividad. Sólo estamos codificando la gravedad como geometría del espacio-tiempo para que la 1ª Ley de Newton pueda ser aplicable.

3. Axiomas geométricos del espaciotiempo Newtoniano

Ahora que entendemos que existe una relación entre la gravedad y la geometría del espaciotiempo de Newton vamos a establecer 3 axiomas sobre esta nueva variedad, olvidando por un momento todo lo aprendido en la sección 2.

Partimos de una variedad $(M,\theta,A)$ diferenciable de dimensión 4 dotada de una conexión $\nabla$ sobre la que existe un tiempo absoluto $t:M\longrightarrow \mathbb{R}$ suave. ¿Cómo debe ser el tiempo absoluto para mantener la estructura del espaciotiempo de Newton? Lo más sencillo es colocarse en un punto $p\in M$ de la variedad y vamos a ver cómo cambia el tiempo al avanzar en la dirección $\partial_0\in T_pM$. Si $(dt)_p(\partial_0)=0$, el tiempo no avanzaría en esa dirección, y lo mismo podríamos hacer con el resto de coordenadas. Por eso postulamos lo siguiente:

1. $(dt)_p\neq 0 \ \forall p\in M$ implica que $M$ está "foliada" en subconjuntos $S_{\tau}:=\{p\in M:t(p)=\tau\}$ disjuntos tal que  $M=\cup S_{\tau}$. Esto es consecuencia del Teorema de la Función Implícita. De hecho, con estos requerimientos, los conjuntos $S_{\tau}$ son variedades topológicas de dimensión 3 con cartas $(x^1, x^2, x^3)$ diferenciables. Si $(dt)_p=0$ entonces el tiempo moriría o emergería de ese punto, lo cual, lejos de cualquier interpretación abstracta, no tiene sentido físico en Mecánica Newtoniana.

2. El tiempo fluye uniformemente a lo largo de cualquiera de las 4 direcciones del espaciotiempo, o simbólicamente, $\nabla dt = 0$. Esto es equivalente a decir que la 1-forma $dt$ derivada a lo largo de cualquier dirección da la forma nula, lo que implica que cuando yo quiera ver cómo de rápido fluye el tiempo a lo largo de cualquier dirección, el resultado me va a dar lo mismo sobre cualquier punto $p$ de la variedad. El tiempo sólo avanza hacia el futuro (no en el espacio) y de forma constante. No es posible un viaje en el tiempo hacia el pasado.

3. Necesitamos postular también cómo funciona $\nabla$. Tomando coordenadas cartesianas $(x^0, x^1, x^2, x^3)$ sobre la variedad tendremos, como antes, que $\Gamma_{0 0}^{\alpha}:=-f^{\alpha}(x(t))=\partial_{\alpha} U$, siendo $U$ el potencial gravitatorio. En estas coordenadas (y en cualquier otras) ahora podemos calcular la conexión, la curvatura de Riemann, la torsión, etc. La conexión $\nabla$ no tiene torsión, osea que $[\nabla_{\mu},\nabla_{\nu}]V^{\lambda}=Riem_{\mu \nu\rho}^{\lambda}V^{\rho}$. Si tuviésemos torsión, la conexión no sería simétrica y los paralelogramos a lo largo de los ejes coordenados no cerrarían, implicando que al viajar espacios iguales primero en una dirección y luego en otra, no llegaríamos al mismo punto.

Si nos fijamos en los vectores de la base en $T_pM$ y cómo varían al movernos sobre la variedad, observamos que $\nabla_0\partial_0=\Gamma_{0 0}^i\partial_i$. Visualmente, una partícula con velocidad temporal (en reposo en el espacio) se va a acelerar por la curvatura de la variedad hacia donde aumente el campo gravitatorio. Lo mismo podemos deducir si calculamos las derivadas de la base de $T_pM^*$.

Para introducir el concepto de observador necesitamos dotar de una métrica a nuestra variedad. Entonces diríamos que un observador es una curva en el espaciotiempo cuyo vector tangente apunta hacia el futuro, ie $dt(V)>0$, y que porta una elección de base de cada $T_pM$ continua (y ortonormal).

Ahora podemos reformular las leyes de Newton en términos geométricos. Nótese que no necesitamos dotar de una métrica a este espacio, la única estructura adicional ha sido una conexión. Si lees algo más sobre el tema, también puede partirse de un espacio métrico y desarrollar la misma teoría. En este marco, las leyes de Newton quedarían:

1ª Ley: la línea del mundo de una partícula sobre la que no actúan fuerzas (la gravedad no es una fuerza) es una geodésica dirigida hacia el futuro, es decir, $\nabla_V V=0$ con $dt(V)>0$.

2ª Ley: la desviación que sufren las líneas de mundo de las partículas es proporcional a la fuerza, es decir, $\nabla_V V=F/m$ con $dt(F)=0$. Las fuerzas, por tanto, te aceleran en las direcciones espaciales pero no en la temporal.

No hemos definido lo que es un sistema inercial en nuestro espacio-tiempo, ni falta que hace. Simplemente tenemos una variedad topológica dotada de una conexión (que conocemos explícitamente en unas coordenadas determinadas).

Tomemos ahora coordenadas de tal modo que $x^0=t$, igual que antes. Nadie nos lo impide y va a simplificar todo, pues ahora los elementos $\Gamma^0_{a b}$ de la conexión son todos cero, con $a,b=0, 1, 2, 3$. De este modo la 2ª Ley en coordenadas nos dice que la coordenada $x^0$ es proporcional al parámetro que define la curva, y con un cambio adecuado de unidades podemos parametrizar con el tiempo absoluto $t$. 

Si escribimos la 2ª Ley de Newton en coordenadas espaciales vamos a obtener lo siguiente:

$\ddot x^{\alpha}+\Gamma^{\alpha}_{b c}\dot x^c\dot x^d+\Gamma^{\alpha}_{0 0}+2\Gamma^{\alpha}_{0 b}\dot x^b=F^{\alpha}/m$

Donde he separado los términos espaciales de los temporales para que se entienda mejor. El término $\Gamma^{\alpha}_{0 0}$ es el único que aparece en presencia de gravedad (con una buena elección de coordenadas). En ausencia de gravedad, podríamos escoger coordenadas tales que todas las $\Gamma$'s se anulasen (espaciotiempo plano). El resto de términos de la conexión no son gravitatorios, sino debidos a las coordenadas. Son las correciones de Coriolis, Centrípeta... fruto de elegir sistemas rotantes (que son coordenadas fijas en el espaciotiempo). Si escogemos coordenadas cartesianas, en un espacio sin gravedad, tendríamos 

$\ddot x^b=F^b/m$

4. Variedad métrica

Como complemento, vamos a intentar dotar a nuestra variedad de una métrica, de modo que de ella se desprenda la conexión del apartado anterior de forma natural. Sea $(U,x)$ la carta con la que hemos trabajado anteriormente. En estas coordenadas defino la métrica 

$g_{i j}:=diag( -U, 2, 2, 2)_{i j}$

Puedes probar como ejercicio que de esta métrica puede derivarse la conexión de Levi-Civita (determinada unívocamente) y que coincide con la conexión definida en la sección anterior. De este modo dotando a la variedad de este campo métrico, obtenemos todos los resultados de antes.

5. Ejemplos

En primer lugar vamos a estudiar una partícula libre en ausencia de gravedad. Por simplicidad tomemos sólo dos componentes espaciales. Escogiendo coordenadas cartesianas y condiciones iniciales tales que $(t(0)=0,x(0)=x_0,y(0)=y_0)$ y $(\dot t(0)=1,\dot x(0)=a,\dot y(0)=b)$ tendremos, por el primer axioma de Newton (en coordenadas) que $x=at+x_0$ y $y=bt+y_0$. Nada del otro mundo. La variedad es plana, pero escogiendo otras coordenadas (como polares), en la conexión aparecen términos no nulos pero que son un mero artificio. En este caso, $\Gamma^{\phi}_{r \phi}=1/r$ y $\Gamma^r_{\phi \phi}=-r$ de modo que obtendríamos $\ddot\phi+1/r\dot\phi\dot r=0$ y $\ddot r-r\dot\phi^2=0$. No es más que una línea recta en el espacio pero descrita en polares.

La curva para una partícula libre, ahora con gravedad, vendrá dada por la primera ley de Newton. Supongamos una curva $\gamma$ en una carta $(U, x)$, que es aquella en la que la conexión tomaba esa forma tan sencilla, que parte de $(0,H,0,0)$ con vector tangente $(1,0,0,0)$. Evidentemente no podemos anular la conexión escogiendo unas "buenas coordenadas", pues la variedad es curva, ie, $Riem \neq 0$. Dicha curvatura (tensor de Riemann) viene codificada por la densidad de materia del universo. El único elemento no nulo de la conexión es $\Gamma^1_{0 0}=-g$ con $g$ constante a lo largo de la curva. La primera Ley de Newton nos dice que $\nabla_V V=0$, es decir, que la partícula se va a mover en "línea recta" por la variedad. Si resolvemos las ecuaciones (es trivial y lo propongo como ejercicio) en estas coordenadas, obtenemos las del tiro parabólico, es decir, $\gamma_x=(t, H-1/2g t^2, 0, 0)$. Por tanto, en esta geometría, ¡la "línea recta" corresponde a una parábola!

Podemos pasar a unas coordenadas $(y^0, y^1, y^2, y^3)=(y\circ x^{-1})(x^0, x^1, x^2, x^3)=(t, x^1-H+1/2g t^2, x^2, x^3)$, donde la métrica toma la forma $g_{0 0}=-U-2g^2t^2$, $g_{1 0}=g_{0 1}=4gt$, $g_{1 1}=g_{2 2}=g_{3 3}=2$ y el resto nulos. Si calculas los elementos de la conexión, te vas a llevar una sorpresa: todos son cero (en todo punto de la variedad). Esto ocurre porque te la he colado un poquito. Si $g$ fuese constante la variedad sería plana, y esto no es así por la ecuación de Poisson. Si admitimos que $g=g(x^1)$ aún podríamos eliminar la conexión, pero sólo en un punto (o en un conjunto de puntos) de la variedad. Es lo que se denominan coordenadas localmente inerciales.

Vemos por tanto que la conexión es algo ligado al observador (algo así como la sensación de peso) y la curvatura es algo intrínseco a la variedad (que codifica la materia). Dos observadores en un mismo espaciotiempo curvo pueden tener sensaciones de peso muy distintas, como acabamos de comprobar. El observador en caída libre no siente la gravedad (su conexión es nula, coordenadas localmente inerciales) mientras que el observador "en reposo" nota una conexión no nula.

De igual modo, dos observadores en un espaciotiempo plano pueden tener sensaciones muy distintas. Uno inercial no siente la gravedad (la conexión es nula), pero uno acelerado sí (por puro efecto de las coordenadas).

 

6. Conclusiones

La idea básica que subyace es la siguiente: gracias al principio de equivalencia podemos codificar la gravedad como curvatura del espaciotiempo, de modo que dejemos de considerar los efectos de la gravedad como una fuerza y los atribuyamos a una consecuencia de un espaciotiempo curvado. Las geodésicas en esta nueva geometría son las curvas que describen las partículas libres, que no son trayectorias "uniformes y rectas" en el sentido habitual de la expresión. 

En primer lugar hemos definido la conexión de manera constructiva en unas cómodas coordenadas, para después axiomatizar la teoría a partir de la cual podemos hacer física. Con pocos axiomas sobre la conexión y el tiempo absoluto hemos construido el espaciotiempo newtoniano incorporando la gravedad como curvatura del mismo. Del mismo modo podemos axiomatizar la teoría postulando una métrica como la de la sección 4 de la que se puede deducir la conexión.

7. Bibliografía

Newton - Cartan theory on Wikipedia

Newtonian spacetime (Frederic Schuller) of Winter Scohol on gravity and light

The Geometry of Physics (Theodore Frankel)

Introducción a la Geometría Diferencial - Univ. de Granada (M.S.C & J.L.F.D)

Introducción a la Relatividad General - Bert Janssen